LTI   Linear Time Invariant System   선형 시불변 시스템, 선형 시불변, LTI 시스템

1. 선형 시불변 시스템 (LTI, Linear Time Invariant System)

  ㅇ 선형성(중첩의 원리) 및 시불변성(Time-invariant) 특성을 둘다 갖는 시스템

  ※ 대부분의 물리계(시스템)는 비선형시스템이나, 
     - 취급이 편리한 LTI 모델(선형 근사,Linear Approximation)로써 표현,분석,설계 하게됨


2. LTI시스템의 수학적 표현

  ※ [수학적 모델화]
     - LTI시스템 : 상수 계수를 갖는 선형 미분방정식 또는 차분방정식으로 모델화

  ㅇ (연속시스템 표현) → 미분 방정식
     - 시간 영역 표현   :  
     - 주파수 영역 표현 
        . 푸리에 변환 표현 (주파수응답) :  H(jω) = |H(jω)| e∠H(jω)
        . 라플라스 변환 표현 (전달함수) :  

  ㅇ (이산시스템 표현) → 차분 방정식
     - 시간 영역 표현   :  
     - 주파수 영역 표현 
        . DTFT 변환 표현     :  
        . z 변환 표현        :  

  ㅇ (시스템응답 표현) → 입력 및 임펄스응답과의 콘볼루션      ☞ LTI 시스템응답 참조
     


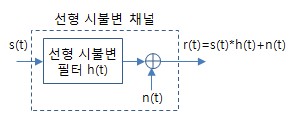
3. LTI시스템의 특징

  ㅇ 중첩의 원리가 성립됨
     - 여러 입력 신호가 모두 합쳐진 결과가, 개별 입력 신호 결과들이 합쳐진 것과 같아짐

  ㅇ 입출력 관계의 표현이 용이함              ☞ LTI 입출력 참조
     - 시간 영역   : `임펄스응답(즉, 콘볼루션 계산)`에 의해, LTI시스템을 완전히 표현 가능
     - 주파수 영역 : `주파수응답  H(jω) 또는 전달함수 H(s),H(z)`에 의해, 표현 가능 
        . 이때의 함수는 유리함수 형태임

  ㅇ 모든 LTI시스템은 인과적임
     - 현재 출력이 현재,과거의 입력에 만 의존하는 성질
        . 현재 응답이 미래 입력을 미리 요구하지 않음
     - 또한, 대부분의 LTI시스템은 메모리 없음 (무 기억성)
        . 메모리(기억성) : 과거,현재,미래가 상호 의존적

  ㅇ 구성요소 간에 교환법칙,결합법칙,분배법칙이 성립함
     - 즉, 콘벌루션 기본 성질과 같음

  ㅇ 콘벌루션 정리가 적용됨
     - 시간 영역 상의 콘벌루션 연산은 주파수 영역 상의 곱셈 연산과 같음
        .  x(t) * h(t) ↔ X(ω) H(ω)
  
  ㅇ 고유함수,고유값에 의해, 선형성 해석에 유익함                  ☞ LTI 고유함수 고유값 참조
     - LTI시스템을 통과해도 기본성질이 변화하지않는 신호 = `고유 함수`
        . 例) 만일, 입력이 정현파이면 (지수 함수, 정현 함수 등),
           .. 주파수는 입력과 동일하나, 진폭과 위상은 달라짐
     - LTI시스템 출력은 특정값에서 고유함수의 복소 상수배가 됨 = `고유값`


4. LTI 특성을 갖는 채널

  ※ ☞ LTI 채널 참조
     - 랜덤 잡음이 가산되고, 대역제한된 필터 특성을 갖는 채널을 말함