Difference Equation 차분 방정식, 차등 방정식 | (2024-05-01) |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
이산 신호/이산 시스템
▷
이산 시스템
▷
이산시스템 표현,구현
▷ Top ▷ 기초과학 ▷ 수학 ▷ 수치해법 ▷ 수치 미분방정식
▷ Top ▷ 기초과학 ▷ 수학 ▷ 수치해법 ▷ 수치 미분방정식
1. 차분 (Difference) 이란? ㅇ 차분 : 임의 두 점에서의 함수 값들의 차이 - 차분 : f(xi+Δx) - f(xi) 또는 fk+1 - fk ㅇ 차분 근사 : 도함수에 대한 근사 * 함수의 미분(도함수)을 차분으로 근사적으로 표현하는 것 - (연속적) 미분 :- (이산적) 차분 근사 :
2. 차분 방정식 (Difference Equation) ㅇ 자연계(System)의 수학적 모델링인 미분방정식의 이산적인(Discrete) 표현 - 이산적 현상에 대한 모델링 . 시간에 따라 이산적으로 나타나는 자연현상 등을 모델링하는 분야에 많이 사용 .. 수치해석, 유한수학, 제어이론, 컴퓨터과학 등 ㅇ 例) 복리 계산, 번식하는 종들의 개체수 증가 등 3. 차분 방정식의 특징 ㅇ 차분 방정식의 형태는, 수열의 점화식과 같은 형태를 취함 - (점화식 例) 피보나치 수열 : an = an-1 + an-2 - 수열의 각 항(項)들에 의해, 규칙적(종속적)으로 구성시킨, 함수 관계식 ㅇ 차분 방정식의 해는, 수열 형태임 - 즉, 차분 방정식을 만족하는 수들로 이루어진 수열 : {#y_0,y_1,y_2,\cdots#} ㅇ 미분방정식의 이산형으로 볼 수 있음 - 미분방정식을 이산적인 함수값에 의해 방정식으로 표현 가능 . 즉, 유한 차분 형식(전향 차분,후향 차분,중앙 차분) 중 하나에 의해, 방정식으로 표현 함 ㅇ 이산시스템의 입출력 관계가 차분 방정식으로 드러남 ☞ 이산 시스템 표현 참조 - 이산시스템 입출력이 현재값,과거값,내부값(계수)으로 구성시켜 표현됨 . 이산적인 입출력의 직접적인 신호 관계를 통해서 얻어지는 시스템 방정식을 표현함 4. 차분 방정식의 표현 例 ㅇ 컨볼루션 합에 의한 표현 例
[# y[n] = h[n] * x[n] = \sum^{\infty}_{k=0} h[n] x[n-k] #]ㅇ 순환필터에 의한 표현 例 - 현재의 출력값에 기여하는, 과거의 출력 및 현재,과거의 입력에 의한 표현[# y[n] = -\sum^N_{k=1} a_ky[n-k] + \sum^M_{k=0} b_kx[n-k] #]. N계 선형 시불변 차분방정식 . y[n] : 출력 . x[n] : 입력 . y[n-k] : 상태 . a,b : 내부값(계수) ㅇ 2차 FIR 필터에 대한 표현 例 - (시간 영역)[# y(nT) = a_0x(nT) + a_1x(nT-T) + a_2x(nT-2T) #]- (z 변환 영역)
[# Y(z) = a_0X(z) + a_1z^{-1}X(z) + a_2z^{-2}X(z) = H(z)X(z) #]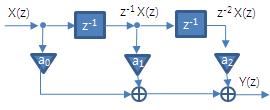
▷이산시스템 표현,구현
1. 이산 시스템 표현 2. 컨볼루션 합 3. 차분 방정식 4. 전달 함수 5. 이산시스템 구현 구조
▷수치 미분방정식
1. 수치 미분방정식 2. 오일러법 3. 차분 방정식 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]