Non linear System, Bilinear 비 선형, 비 선형 시스템 | (2022-07-30) |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
시스템 표현/성질
▷
선형시스템
1. 비 선형 시스템 (Nonlinear System) ㅇ `중첩의 원리(Principle of Supersition)`를 만족하지 않는 시스템(계,field) ㅇ 例) - 비 선형 소자 : 다이오드, 트랜지스터 등 . 선형 해석을 위해서는, 선형화시킨 `등가회로` 참조 - 선형 소자 : 저항, 인덕터, 커패시터 등 선형 수동 소자 2. 비 선형 시스템의 특징 및 사례 ㅇ 입출력 신호 관계가 선형성 조건을 만족하지 않음 - 제곱(포물선), 삼각함수, 지수함수 등의 입출력 관계를 갖는 시스템은 비 선형 시스템 . x², x dx/dt , cot x , ex, 1/x 등 ㅇ 평행 이동 - f(x) = ax + b ☞ 아핀함수 참조 . 일직선(선형성의 특징 중 하나)임에도 불구하고 절편이 있어서 비 선형적임 - 초기조건이 영이 아니거나,오프셋을 갖거나(데드존 영역),포화영역 등이 있는 경우 . 동작영역 중에 비 선형 구간이 있는 경우ㅇ 양 선형 (Bilinear) - 구간별로는 선형이나, 전체적으로는 비 선형으로 간주됨
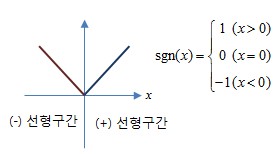
▷선형시스템
1. 선형 2. 비선형 3. 중첩의 원리 4. 선형 벡터공간 5. 선형 방정식 6. 선형 미분방정식 7. 선형 결합 8. 선형 연산