Complex Frequency, Complex Variable   복소 주파수, 복소수 변수, 복소 변수

1. 복소 변수, 복소 함수

  ㅇ 복소수 변수 (Complex Variable)
     - 두 실수 변수 x,y 의 순서쌍  z = (x,y)
        . 실수부,허수부,허수단위(j)로 표현되는 복소수 변수  z = x + jy
     - 복소 평면 상의 한 점으로 나타낼 수 있음

  ㅇ 복소수 함수 (Complex Function)
     - 모든 복소수 z 값에 대응하는 f(z) 값이 존재하는 함수


2. 복소 주파수

  ㅇ (명칭) 복소 주파수(Complex Frequency) / 복소 변수(Complex Variable) / 복소 주파수 변수

  ㅇ 주파수를 변수 성분으로써 갖는 복소수 형태의 변수  
     - 주파수에 따른 복잡한 시스템응답 등을 보다 쉽게 표현하기위한 수단

  ㅇ 복소 주파수 표현의 장점
     - 즉, 시간 t의 함수인 임펄스응답 h(t) 만으로 다루는, 시간영역에서의 취급 보다,
        . 복소주파수/복소변수의 `복소 함수` H(s) (s=σ＋jω) 또는 H(z) (z=eσ＋jω=r ejω) 및
        . 이에따른 `복소 평면`을 도입하여 다루는 것이 훨씬 편리하고 유용


3. 복소 주파수의 영역 표현

  ㅇ 복소 주파수 영역 (Complex Frequency Domain)
     - 복소 주파수의 변화 양상(동태)에 따라 시스템을 해석하게되는 영역(분야)

  ㅇ 복소 주파수 평면 (s 평면 또는 z 평면) (Complex Frequency Plane)
     - 복소 주파수 실수부,허수부를 직각 좌표계에 대응시켜 표현한 평면

  ㅇ 복소 변환 영역
     - 복소 변수에 의해 간단한 대수적 표현이 가능한 변환영역
        . 연속신호인 경우에, ☞ 라플라스 변환 참조
        . 이산신호인 경우에, ☞ z 변환 참조


4. 복소 주파수 변수의 구분

  ㅇ 연속 신호에 대응
     - 복소 주파수/복소 변수 :  s = σ＋jω
       

  ㅇ 이산 신호에 대응
     - 복소 주파수/복소 변수 :  z = r ejω
       


5. 연속 신호(시간영역) 대비 복소 평면(변환영역) 표현 例)

  ㅇ 지수(指數)적으로 감소하는 신호
      
  ㅇ 지수(指數)적으로 증가하는 신호
      
  ㅇ 정현파적으로 진동하는 신호
      
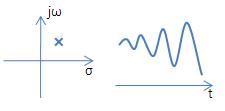
  ㅇ 정현파적으로 진동하며 지수 감소하는 신호
      
  ㅇ 정현파적으로 진동하며 지수 증가하는 신호
      

1. ▷ Top (분류 펼침)      :     1,591개 분류    6,514건 해설 검색 펼침