라플라스 변환 성질, 라플라스 변환 주요 특성 | (2021-03-14) |
초기값 정리, 최종값 정리 | |
▷
Top
▷
신호/시스템
▷
변환 해석
▷
라플라스 변환
1. 라플라스 변환 주요 특성 ㅇ 선형성 (Linearity)[# L\left[ \; k_1f_1(t) + k_2f_2(t) \; \right] = k_1F_1(s) + k_2F_2(s) #]ㅇ 주파수 천이 (Frequency Shift) 및 시간 천이 (Time Shift)[# L\left[ \; e^{s_ot}f(t) \; \right] = F(s - s_o) #][# L\left[ \; f(t - t_o) \; \right] = e^{-st_o}F(s) #]ㅇ 시간비율변화 (Time Scaling)[# L\left[ \; f(at) \; \right] = \frac{1}{|a|} F\left(\frac{s}{a}\right) #]ㅇ 미분, 적분 (unilateral,one-sided 인 경우)[# L\left[ \frac{df}{dt} \right] = sF(s) - f(0^-) \\ L\left[ \frac{d^2f}{dt^2} \right] = s^2F(s) - sf(0^-) - f'(0^-) \\ L\left[ \frac{d^nf}{dt^n} \right] = s^nF(s) - s^{n-1}f(0^-) - s^{n-2}f'(0^-) - \cdots - f^{(n-1)}(0^-) \\ \qquad\qquad = s^nF(s) - \sum^n_{k=1} s^{n-k}f^{(k-1)}(0^-) #][# L\left[ \int^t_{0^-} f(τ)dτ \right] = \frac{F(s)}{s} \\ L\left[ \int^t_{-\infty} f(τ)dτ \right] = \frac{F(s)}{s} + \frac{1}{s}\int^{0^-}_{-\infty} f(τ)dτ #]ㅇ 초기치 정리(초기값 정리), 최종치 정리(최종값 정리)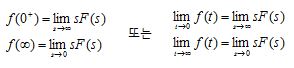
▷라플라스 변환
1. 라플라스 변환 2. 복소 주파수 3. 라플라스 변환쌍 4. 라플라스 변환 성질 5. 라플라스 변환 가능 6. 부분분수 전개 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]