CTFS Fourier Series, Continuous Time Fourier Series 푸리에 급수, 연속시간 푸리에급수 | (2023-05-23) |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
수열,급수
▷
멱급수
▷ Top ▷ 신호/시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에 급수
▷ Top ▷ 신호/시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에변환 표현 종류
▷ Top ▷ 신호/시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에 급수
▷ Top ▷ 신호/시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에변환 표현 종류
1. 푸리에 급수 (Fourier Series) ㅇ 임의 주기 신호를 서로다른 주파수의 정현파(또는 지수신호) 성분들의 합으로 표현한 것 2. 푸리에 급수의 표현 상의 특징 ㅇ 정현파 성분들의 중첩 표현 - 거의 대부분의 신호는 정현파(또는 지수신호) 성분들의 중첩으로 표현할 수 있음 . 특히, 주기적인 신호일 경우에는, 기본주파수의 정수배로된 일련의 정현파들의 크기 와 위상을 적절히 합성함으로써 표현 가능 - 결국, 주기 신호들은 정현파신호(또는 복소지수신호)들의 무한 급수로 표현 가능 ㅇ 주기 신호를 표현하는 기본적인 도구 - 연속시간 주기신호 => 무한 개 길이의 푸리에급수 (연속시간 푸리에급수, CTFS) . 그 기본주파수의 정수배 주파수를 갖는 정현파들의 크기 및 위상을 적절히 조절하여 무한개 더함으로써 합성이 가능 - 이산시간 주기신호 => 유한 개 길이의 푸리에급수 (이산시간 푸리에급수, DTFS) . 유한 개 길이의 푸리에 급수로 표현이 가능 - 한편, 비주기적인 신호의 경우에, 적분형식을 갖는 푸리에 변환으로 표현이 가능 3. 푸리에 급수의 주요 응용 ㅇ 시간 신호의 주파수 응답 해석을 위한 응용 도구 - 선형 회로(Linear Circuit)의 응답을 예견하는데 편리 . 이를 주파수 응답(Frequency Response)의 개념으로 확장시킬 수 있음 - 즉, 임의의 신호가 선형회로(선형시스템)를 통과할 때, . 푸리에 급수는 각각의 단일 주파수로된 정현파들의 중첩(중첩의 원리)으로 그 응답을 유도할 수 있음 4. 푸리에 급수의 전개 ㅇ `연속시간 주기신호(T 주기)`에 대한 푸리에급수 전개 표현 (CTFS)[# x_T(t) = \sum^{\infty}_{n=-\infty} c_n e^{jnω_ot} = \sum^{\infty}_{n=-\infty} c_n e^{jn2πt/T} = \sum^{\infty}_{n=-\infty} c_n e^{jn2πft} \\ c_n = \frac{1}{T} \int^T_O x(t) e^{-j2πfnt} dt = |c_n| e^{jθ_n} #]- 여기서, (cn : 복소 푸리에 계수 Fourier Cofficient) - 즉, 연속시간 주기신호(T 주기)를, . 같은 주기(T)를 갖는 복소 고조파(cnejnωt)의, 무한 합(Σ)으로 표현 가능 ㅇ `이산시간 주기신호(N 주기)`에 대한 푸리에급수 전개 표현 (DTFS)- 이산시간 주기신호(N 주기)를 N개의 고조파의 합으로 표현 ㅇ 일반화 함수에 의한 푸리에급수 전개 표현
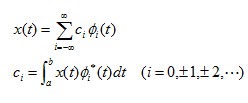
▷멱급수
1. 멱 급수 2. 멱급수 공식 3. 삼각 급수 4. 테일러 급수 5. 푸리에 급수
▷푸리에 급수
1. CTFS(연속시간 푸리에 급수) 2. DTFS(이산시간 푸리에급수) 3. 푸리에급수 표현 예
▷푸리에변환 표현 종류
1. CTFS(연속시간 푸리에급수) 2. CTFT(연속시간 푸리에변환) 3. DTFS(이산시간 푸리에급수) 4. DTFT(이산시간 푸리에변환) 5. DFT(이산푸리에변환) 6. FFT(고속푸리에변환) 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]