Exponential Distribution 지수 분포, 지수 확률분포 | (2025-10-16) |
Exponential Random Variable, 지수 확률변수 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 모형,분포
▷
연속확률분포
1. 지수 분포 (Exponential Distribution) ㅇ 어떤 사건이 처음 발생할 때까지의 경과 시간에 대한 연속확률분포 - 즉, 사건과 사건 사이의 `경과된 시간`에 대한 확률 분포 . 例) 인접 사건 간의 시간 간격에 대한 확률 분포 . 例) 어느 기간 동안 사건이 한번도 안 일어날 확률에 대한 분포 ㅇ 활용 - 창구에서 평균 대기시간, 도착간 시간(Inter-arrival time), 고장과 관련된 수명 (고장율) 등을 모형화하는데 적합한 확률분포 ㅇ 분포 모양 - 지수 형태 (λe-λx)의 분포모양을 갖음 2. 지수 분포의 특성 ㅇ 표기 : X ~ Exp(λ) - λ : 모수 (단위 시간 동안 발생하는 평균 사건 수) ㅇ 확률밀도함수 - 모수 λ > 0 에 의해 결정됨, 지수감소(exponential decay) 형태를 갖음.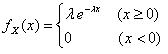
ㅇ 누적분포함수
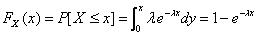
ㅇ 기대값
ㅇ 분산(Variance)
ㅇ 표준편차
3. 지수 분포에서 건망증 또는 무기억성 (Memoryless) ㅇ 어떤 장치가 고장나지 않았다는 조건하에서 나머지 수명은, 그 시간 이전의 그 장치의 수명에 대한 확률밀도함수와 같아짐 ㅇ 즉, 그 시간 경과한 후에 마치 0 시점에서 새로 시작하는 것처럼 행동함 4. 지수 분포와 타 분포와의 비교 ㅇ 지수분포는, 포아송분포 (Poission)의 변형 - 포아송분포 (단위 시간 내 발생 확률 분포) : {# p_X(x) = \dfrac{λ^x e^{-λ}}{x!} #} - 만일, 평균 사건 수를 λ라고 가정하면, t 단위 시간 내, 평균 사건 발생 수는 tλ 임 - 단, (0,t) 시간 동안 사건이 안 일어날 (x = 0) 확률은, {# p_X(0) = \dfrac{(λt)^0 e^{-λt}}{0!} = e^{-λt} #} - 따라서, t 시간 경과 후 최초 사건 발생 확률은, {# P(X > t) = e^{-λt} #} - 결국, 지수분포 (경과 시간 후, 최초 발생 확률 분포)의 누적분포함수, 확률밀도함수는, . {# P(X \leq t) = F(t) = 1 - e^{-λt} #} . {# f_X(t) = dF(t)/dt = λe^{-λt} #} ㅇ 감마 분포 (Gamma) - 어떤 사건과 k번째 후의 사건과의 시간간격을 나타냄 . 사건이 k회 일어날 때까지 걸리는 시간 분포 - 지수분포를 일반화한 것 - 지수분포와 달리 기억성을 갖음 ㅇ 와이블 분포 (Weibull) - 지수 분포를 보다 일반화시켜, 여러 다양한 확률분포 형태를 모두 나타낼 수 있도록 고안됨
▷연속확률분포
1. 연속 확률분포 요약 2. 연속 균등분포 3. Rayleigh 분포 4. Rician 분포 5. 감마 분포 6. 베타 분포 7. 지수 분포 8. 얼랑 분포 9. 와이블 분포 10. 카이제곱 분포(χ² 분포) 11. t 분포 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]