Multivariate Normal Distribution 다변량 정규분포, 다변수 정규분포 | (2024-11-14) |
Bivarate Normal Distribution, 이변량 정규분포, 두 변수 가우시안 랜덤변수, Multivariate Gaussian Distribution, 다변량 가우시안 분포, 다변수 가우시안 분포 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 모형,분포
▷
정규분포
1. 다변량 가우시안 분포, 다변량 정규 분포 ㅇ 여러 변량들을 함께 고려하며, ☞ 다변량 함수, 다변량 확률변수 참조 - 각 변량들이 가우시안 분포를 따르며, ☞ 가우시안 분포(정규 분포) 참조 - 이들간에 상호 상관관계를 가지게 되는, ☞ 상관관계 참조 - 그러한 경우를 다룸 ☞ 확률 모형(확률 분포) 참조 2. 다변량 가우시안 분포의 확률 밀도 함수[# f(X_1,\cdots,X_n) = \frac{1}{\sqrt{(2\pi)^n|\mathbf{Σ}|}} \; \exp \left( -\frac{1}{2} (\mathbf{X}-\mathbf{μ})^T \mathbf{Σ}^{-1} (\mathbf{X}-\mathbf{μ}) \right) #]ㅇ {#n#} : 차원(좌표,확률변수) 수 ㅇ {#\mathbf{X}=(X_1,X_2,\cdots,X_n)^T#} : n 차원 확률변수 즉, 확률벡터 (다변량 확률변수) - (확률벡터 : 다변량 확률변수를 벡터로 표기한 것) ㅇ {#X \sim N(\mathbf{μ},\mathbf{Σ})#} : n 변량 {#X#}가 따르는 정규분포(n 차원 정규분포)에 대한 표기 - 두 개의 모수 {#μ#} (평균벡터), {#Σ#} (공분산행렬)에 의해 결정되는 확률적 분포를 나타냄 ㅇ {#f(X_1,\cdots,X_n)#} : n 차원 확률변수 즉, 확률벡터의 결합 확률밀도함수 - (결합 확률밀도함수 : 2 이상의 이산확률변수들을 동시에 함께 고려하는 결합분포 함수) * [참고] . 가우스 함수 :[# f(x) = \frac{1}{\sqrt{2π}} e^{-\frac{x^2}{2}} #]. 1차원 가우스 분포(정규 분포)의 확률밀도함수 :[# f_X(x) = \frac{1}{σ\sqrt{2π}}\;e^{-\frac{(x-μ)^2}{2\,σ^2}} #].. (X : 확률변수, μ : 평균, σ : 표준편차, σ2 : 분산) ㅇ {#\mathbf{Σ}#} : 공분산 행렬 (Covariance Matrix) - 2 이상의 변량들에서, 변량 값들 간의 공분산(또는 상관계수)들을 행렬로 표현한 것 ㅇ {#|\mathbf{Σ}|#} : 공분산 행렬의 행렬식 (Determinant) - (행렬식 : 행렬(주로,정방행렬)을 하나의 수로써 대응시킴) ㅇ {#Σ^{-1}#} : 공분산 행렬의 역행렬 (Inverse Matrix) - (역행렬 : 실수에서의 곱셈 역원과 유사) ㅇ {#( )^T#} : 전치 (Transposition) - (전치 행렬 : 모든 행과 열을 바꾼 행렬, A = [aij] ↔ AT = [aji] ) ㅇ {#\mathbf{μ}=(μ_1,μ_2,\cdots,μ_n)^T#} : 평균 벡터 (Mean Vector) - 각각의 차원(좌표) 마다 평균한 것(즉,기대값)들을 모아서, 벡터화한 것 ※ [참고] ☞ 위키피디아 (Multivariate normal distribution) 참조 3. 다변량 가우시안 분포의 성질 ㅇ 선형변환에 대해 닫혀있음 - (y = Ax + b 변환 시, 또하나의 새로운 가우시안 분포가 됨) ㅇ 주변분포와 조건부분포도 가우시안 분포임 ㅇ 등고선이 타원 형태를 가짐 4. 例) 2 변량일 때의, 가우시안 랜덤변수의 결합확률분포 ㅇ 2개의 가우시안 확률변수가 결합되어 나타내는 이변량 정규분포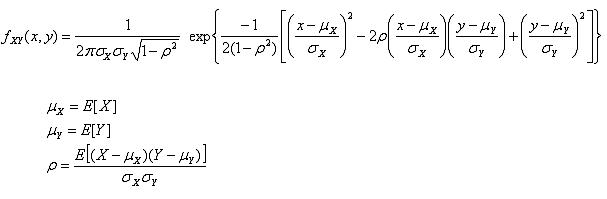
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]