Real Number   실수 (實數)

1. 실수(實數) (Real Number) 이란?

  ㅇ 실수(實數) (Real Number) : ℝ
     - 허수를 제외한 유리수,무리수를 총칭하는 수

    

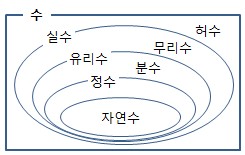  ※ 실수 보다 더 확장된 수 ☞ 복소수 참조


2. 실수(實數)  의 분류

  ㅇ 유리수 (Rational number) :  ℚ  =  { p/q | p,q ∈ Z, q≠0 }
     - 두 정수의 비(比) 즉, 분수(分數)로 나타낼 수 있는 수

     - 정수 (Integer) :  ℤ  =  { ...,-2,-1,0,1,2,... }
        . 양의 정수(Positive Number) = 자연수(Natural Number) :  N = { 1,2,3,... }
        . 영 : {0}
        . 음의 정수 = 음수(Negative Number) : {-1,-2,-3,...}

     - 분수 (Fraction, 分數, 분율, 分率) : 두 수의 비(比)
        . 진분수(proper fraction)   : 분자가 분모 보다 더 작은 분수
        . 가분수(improper fraction) : 븐자가 분모 보다 더 큰 분수
        . 번분수(complex fraction)  : 분모,분자에 분수식이 포함되는 복잡한 분수

  ㅇ 무리수 (Irrational Number) :  I
     - 두 정수의 비(比, 분수)로 나타낼 수 없는 수

     - 비순환 무한소수
        . 제곱근 : ±√2 = ±1.4142135... , ±√3, ...
        . 원주율, 삼각함수 값 : ±π,±sin 20˚, ...

  ※ 한편, 분수(分數) 및 소수(小數)는 표현 방식 차이 외에, 표현 범위도 다름 ☞ 분수 소수 참조
     - (유리수는 분수로 표시 가능하나, 무리수는 분수로 표시 불가능하고 소수로 개략 표현)


3. 실수의 법칙 

  ㅇ 교환법칙 성립  :  a + b = b + a,  a b = b a
  ㅇ 결합법칙 성립  :  a + (b + c) = (a + b) + c,  a (b c) = (a b) c
  ㅇ 분배법칙 성립  :  a (b + c) = a b + a c,  (b + c) a = b a + c a

  ※ 실수 및 연산들이 서로 엮어지는 성질들을 나타냄


4. 실수계(Real Number System)의 공리적 구성

  ㅇ 체 공리 (Field Axiom)
     - 실수 원소의 집합 및 연산으로 엮어진 대수적 구조에 관한 공리

  ㅇ 순서 공리(Order Axiom) 또는 순서배열원리(Ordering Principle)
     - 모든 두 실수는 크기 순서로 배열 가능

  ㅇ 선택 공리(Choice Axiom) 또는 완전 정렬성 원리 (Well-ordering Principle)
     - 모든 가능한 부분 집합 마다 대표 원소들을 동시에 대응(선출)시킬 수 있다는 공리
     - 항상 가장 작은 것이 존재함 또는 선택 가능함

  ㅇ 완비성 공리 (Completeness Axiom)
     - 빈틈(빠진점)이 없음
        . 유리수와 실수를 구분해주는 가장 큰 특징
        . 실수를 이해하려면 극한의 개념이 필요
        . 함수의 연속성을 다룰 때 기초가 되는 성질