검정 판단 기준 | (2024-06-21) |
양측 검정, 단측 검정, Rejection Region, 기각역, 기각영역, Acceptance Region, 수용역, 채택역(x) | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
통계학
▷
통계적 추론
▷
검정
1. 검정의 판단 기준 ㅇ 표본 관측 결과(검정통계량)가 나타난 위치에 의거 판단함 - 표본 관측 결과(검정통계량)가 귀무가설 기각역에 포함 여부에 따라, - 귀무가설의 수용(Accept),기각(Reject)을 결정하게 됨 ※ 사실상, 어떤 기각영역을 취하는 가에 따라, 검정법이 보다 구체화 되어짐 2. 검정 판단을 위한 기준 값 및 범위 ㅇ (기준 값) => 임계값 (Critical Value) 또는 기각치 (Reject Value) - 귀무가설을 기각하는 기준이 되는 값 ㅇ (기각 범위) => 기각역/기각영역 (Rejection Region) - 위 임계값을 중심으로, 귀무가설을 기각시키는 범위 - 즉, 귀무가설이 틀렸다고 판단되는 (기각시킬 수 있는, 대립가설이 유리해지는) 범위 . 발생할 가능성이 매우 희박한 상황 범위 - 구체적으로, . 검정통계량이 유의수준 이하의 매우 작은 확률 .. (유의수준 : 귀무가설이 `의심스러운` 확률 수준, 통상 1%,5% 등) .. 작은 확률 인데도 불구하고 일어났다면, .. 우연으로 보기 어렵다는 상식적인 확률 - 따라서, 이 범위에서 관측값이 나타나는 경우에, . 의심스러운 귀무가설을 버리고, . 주장하고픈 대립가설을 채택할 수 있게 됨 ㅇ (수용 범위) => 수용역/수용영역 (Acceptance Region), 채택역(x) - 임계값을 중심으로, 귀무가설을 수용하는 범위 . (귀무가설의 `채택` 보다는 `수용` 또는 `기각할 수 없음`이라는 용어가 더 적절함) - 이 범위에서 관측값이 나타나는 경우에, 주장하고픈 대립가설을 더이상 주장할 수 없게 됨3. 검정 판단의 기준이 한쪽 만 또는 양쪽인 경우 ※ 기각영역이, 단일 (단측 검정) 또는 양쪽 2개 (양측 검정) 인지에 따른 구분 - 즉, 대립가설의 설정형태에 따라, . 단측 검정({# μ<μ_0 #} 또는 {# μ>μ_0 #}), 양측 검정({# μ \neq μ_0 #}) 으로 구분 ㅇ 단측 검정 (one-tailed test, one-sided test) - 귀무가설의 기각영역이, 검정통계량 확률분포에서 한쪽 끝에 만 있는 경우 . 즉, 기각역이 왼쪽 끝 또는 오른쪽 끝 두 경우가 있을 수 있음 ㅇ 양측 검정 (two-tailed test) - 귀무가설의 기각영역이, 검정통계량 확률분포에서 양쪽 끝에 있는 경우 ※ 例) 모 평균 μ의 검정 - 검정통계량 : 표본 평균 {#\overline{X}#} - 대립가설 {#H_1#}이 설정된 형태에 따라 다음 3가지 경우가 가능 . 하측 단측 검정 :
[# \left\{ \begin{array}{l} H_0 : μ = \overline{X} \\ H_1 : μ < \overline{X} \end{array} \right. #]. 상측 단측 검정 :[# \left\{ \begin{array}{l} H_0 : μ = \overline{X} \\ H_1 : μ > \overline{X} \end{array} \right. #]. 양측 검정 :[# \left\{ \begin{array}{l} H_0 : μ = \overline{X} \\ H_1 : μ \neq \overline{X} \end{array} \right. #]※ [그림 참고] ☞ 위키피디아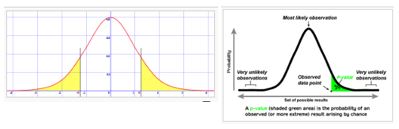
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]