Dirichlet Condition Dirichlet 조건, 디리클레 조건 | (2023-10-26) |
Fourier Transformable, 푸리에 변환 가능, 푸리에 변환 존재성 | |
▷
Top
▷
신호/시스템
▷
변환 해석
▷
푸리에 변환
▷
푸리에 변환 성질
1. Dirichlet Condition ㅇ 푸리에 급수, 푸리에 변환 등이 어떤 함수로 수렴할 충분조건 셋(3) - 단가 함수 (Single-valued) - 유한개 불연속점 (Finite Discontinuities) - 절대 적분가능 (Absolutely Integrable) . 즉,.. x(t)는 전 시간구간에 대해 절대적분가능(absolutely integrable)해야함 ㅇ 디리클레 조건은 충분조건이지 필요조건은 아님 2. 푸리에 변환 가능 ㅇ 푸리에 변환은, 모든 신호에 대해, 주파수 영역 함수로 수렴시켜 표현 가능하지 않음. - 에너지가 유한한 에너지 신호, 전력이 유한한 전력 신호 등, 특별한 신호에 한해 변환 가능하며, - 라플라스 변환 보다는 표현이 가능한 신호가 제한적임 ㅇ 푸리에 변환 가능 (수렴성) : Dirichlet 조건을 만족할 때 3. Dirichlet 조건은 만족시키지 않지만, 그래도 변환이 존재하는 유용한 신호 ㅇ 임펄스 신호 :
ㅇ 단위계단신호 :
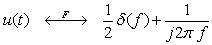
▷푸리에 변환 성질
1. 푸리에 변환의 성질 2. 푸리에 변환의 시간 주파수 관계 3. 푸리에 변환 쌍 4. 해석적, 인과적 신호 5. Dirichlet 조건 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]