Markov Process, Markov Chain 마르코프 프로세스, 마르코프 과정, 마코브 과정, 마르코프 모델, 마르코프 연쇄 | (2025-07-31) |
마르코프 체인, 마코프 체인, 마르코프 가정 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 과정
▷
특별한 랜덤과정
▷
마르코프 과정
1. 마르코프 과정/프로세스 (Markov Process) ㅇ 복잡한 확률과정을 단순한 가정으로 접근 함 - 미래 결과가, 오직 현재(직전) 시점에 만 의존하며, 과거 시점에는 의존 안함 * 마르코프 가정 . Xi+1이, 직전 Xi에 만 영향을 받고, 그이전 X1,X2,...,Xi-1과는 통계적 독립 ㅇ 즉, 어떤 상태로 들어갈 확률이, 들어가기 직전 상태에 만 의존하는 확률과정(랜덤 과정) - 결국, 다음에 나올 상태에 대한 확률 값이, . 오로지, 직전 과거에 만 종속됨 . 따라서, 그 이전 과거의 역사와는 무관 ※ Andrei Andreyevich Markov (1856~1922) - 러시아 수학자. 확률론 업적으로 유명. 2. 과거 상태와 상관성이 있는 경우의 例) ㅇ 일반적으로, 문장(文章) 내에서 연이어나올 글자,구절들이 서로 상관성을 갖음 - 이를 메모리 요소가 있다고 함 ㅇ 만일, 신호 주파수 스펙트럼 상에서 특정 주파수대에 몰려있으면, - 이 신호는, 시간적으로 상관성을 가진다고 볼 수 있으며, - 시간적 상관성을 갖는 신호는, 모두 메모리를 갖는다고 말할 수 있음 3. 마르코프 연쇄 (Markov Chain) 이란? ㅇ 마코브 과정에서 이산적인 경우 만 고려한 경우 ㅇ 마르코프 연쇄의 특징 - 각 시행의 결과는, 바로 직전 시행의 결과에 만 영향을 받음 - 각 시행의 결과가, 미리 정해진 여러 결과 중의 하나가 됨 4. 마르코프 연쇄의 차수 (확장) ㅇ 내부에 갖고있는 기억 요소의 개수 - 1차 마르크프 연쇄 : 직전 과거 값 만이 현재 값에 영향을 줌 - m차 마르크프 연쇄 : 과거 m개 값이 현재 값에 영향을 줌 . 例) yn+1 = xn + xn-1 .. 2-memory를 갖는 차수 2의 마르코프 과정 例 .. 과거 2개의 값이 현재 값에 영향을 줌 5. 마르코프 연쇄의 구성 ㅇ (상태들의 집합) + (상태들 간의 천이 확률) - 상태들의 집합 (Set of States) . 계가 가질 수 있는 모든 가능한 상태들의 모임 .. 例) 날씨 모델이면, S = {맑음(Sunny), 흐림(Cloudy), 비(Rainy)} . 각 시점 n에서, 계는 이 중 하나의 상태에만 존재 - 상태 천이 확률 (State Transition Probability) ☞ 아래 7,.항 참조 . 한 상태에서 다른 상태로 이동할 확률적 규칙을 정의 .. 이 확률들은 천이 확률 행렬 (Transition Probability Matrix) 로 표현 가능 6. 마르코프 연쇄의 정상성 (Stationary) ㅇ 마르코프 연쇄의 천이 확률은 시점과 무관하게 일정 함 - 즉, P(X2 = j | X1 = i) = P(X3 = j | X2 = i) = P(X4 = j | X3 = i) = … . 통계적 성질이 시간에 따라 변하지 않음 . 여러 시간 구간 마다 모두 동일한 통계적 특성을 갖음 7. 마르코프 연쇄의 표현 ㅇ 마르코프 연쇄의 행렬에 의한 `식 표현` => 행렬 벡터 곱 - 일정 시간 간격 (상태) 마다 반복 천이되며, 천이확률이 매 천이 마다 동일함 . 이러한 연쇄(Chain)를 설명하는 확률 행렬을 확률 천이 행렬이라고 함 - 행렬 벡터 곱 표현 : {# \mathbf{x}(k+1) = \mathbf{P}\;\mathbf{x}(k) #}. x(k) : 상태벡터 (State Vector) . P : 확률 천이 행렬/천이 행렬/확률 행렬 (Probability Transition Matrix) . pij : 천이확률 (Transition Probability) ㅇ 마르코프 연쇄의 상태의 `계산 표현` => 반복 계산 - 임의 시각의 상태 x(k+1)까지 반복적으로 계산할 수 있음
[# x(1) = P\,x(0),\;x(2) = P\,x(1),\;\cdots\;,x(k+1)=P\,x(k) #]. 즉, 천이확률과 초기 상태벡터에 의해 완전히 결정됨 ㅇ 마르코프 연쇄의 `그림 표현` => 천이 그래프 - 천이 그래프 (Transition Graph) / 상태 천이도 (State Transition Diagram) . 각 상태 사이의 천이확률들을 방향 그래프로 표현 .. (천이확률 : j 상태에서 i 상태로 천이되는 확률 : pij = P[ Xn+1=i | Xn=j ]) - 상태천이도 및 천이행렬 例)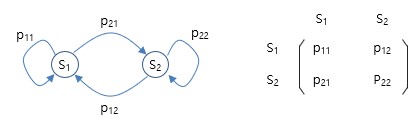
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]