Partial-fraction Expansion 부분분수 전개 | (2024-09-28) |
부분분수 분해 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
변환 해석
▷
라플라스 변환
1. 부분분수 전개 (Partial-fraction Expansion) ㅇ 통상, 시스템함수 또는 전달함수는, s 또는 z의 다항식의 유리함수로 표현된, 복잡한 함수 형태임 ㅇ 따라서, 복잡한 함수의 라플라스 또는 z 역변환을 보다 쉽게 구하기 위해, ㅇ 라플라스 또는 z 역변환을, 이미 알고있는, 간단한 부분분수 항들의 합으로 나타내는 것 ※ 헤비사이드 부분분수 분해 (Heaviside Cover-up Method, 헤비사이드 커버업 기법) - 복잡한 형태의 분수식을 2 이상의 분수식으로 쪼개는 기법으로, - 쪼개진 각 부분분수 항의 계수를 간편하게 구할 수 있음 * Oliver Heaviside (1850~1925) : 영국 전기기술자,물리학자 등 독학자 2. 부분분수 전개의 종류 ㅇ 함수 F(s)의 분모 다항식이, 서로 다른 실근(단순 실근)을 갖는 경우 (distinct)ㅇ 함수 F(s)의 분모 다항식이, 실수인 중근을 포함하는 경우 (equal,multiple)
ㅇ 함수 F(s)의 분모 다항식이, 복소수 근이나 순 허근을 갖는 경우 (complex conjugate)
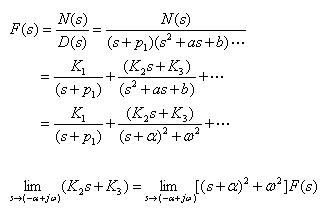
▷라플라스 변환
1. 라플라스 변환 2. 복소 주파수 3. 라플라스 변환쌍 4. 라플라스 변환 성질 5. 라플라스 변환 가능 6. 부분분수 전개 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]