XOR, XNOR Exclusive-OR, Exclusive-NOR XOR 게이트, XNOR 게이트, 배타적-OR 게이트 | (2024-09-16) |
배타적 논리합, 배타 논리 합 | |
▷
Top
▷
전기전자공학
▷
디지털공학
▷
논리 게이트
1. XOR (Exclusive-OR) 게이트 ㅇ 입력이 같으면 `0`, 다르면 `1`의 출력이 나오는 소자 - 입력 중 어느 하나 만 1일 경우에 만 출력이 1이 되는 소자ㅇ XOR의 논리 연산식 : {#x \oplus y = x'y + xy' #} ㅇ XOR의 항등식 - x ⊕ 0 = x - x ⊕ 1 = x' - x ⊕ x = 0 - x ⊕ x' = 1 - x ⊕ y' = x' ⊕ y = (x ⊕ y)' ㅇ XOR의 연산 성질 - 교환법칙 성립 : {# A \oplus B = B \oplus A #} - 결합법칙 성립 : {# (A \oplus B) \oplus C = A \oplus (B \oplus C) = A \oplus B \oplus C #} ㅇ XOR의 대수적 특징 ☞ 모듈러-2 덧셈 참조 - 연산 : 0 ⊕ 0 = 0, 0 ⊕ 1 = 1, 1 ⊕ 0 = 1, 1 ⊕ 1 = 0 . 같으면 `0`, 다르면 `1` - 항등원 : 0 (e ⊕ a = a ⊕ e = a) - 역원 : 0의 역원은 0, 1의 역원은 1 이 됨 (각 원소의 역원이 자기자신이 됨) . (a ⊕ a-1 = a-1 ⊕ a = e : 0 ⊕ 0 = 0, 1 ⊕ 1 = 0) - 어떤 값에 동일한 값으로 두 번 XOR 하면 원래 값으로 됨 : (a ⊕ (a ⊕ b)) = b . (1 ⊕ (1 ⊕ 1)) = 1 : 1 ⊕ 1 = 0 → 1 ⊕ 0 = 1 .. (1에 1을 XOR하여 나온 0에 다시 1을 XOR하면 원래 1이 됨) . (0 ⊕ (0 ⊕ 1)) = 1 : 0 ⊕ 1 = 1 → 0 ⊕ 1 = 1 .. (1에 0을 XOR하여 나온 1에 다시 0을 XOR하면 원래 1이 됨) ㅇ XOR의 게이트 IC 例) 7486 등 ㅇ 응용 : 논리 가산기, 모듈러-2 덧셈 등 2. XNOR (Exclusive-NOR) 게이트 ㅇ 입력이 같을 경우에 만 `1`의 출력이 나오는 소자 - 때론, 항등 게이트(Equivalence) 라고도 함
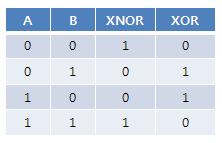
ㅇ XNOR 논리 연산식 : {#x \odot y = (x \oplus y)' = xy + x'y' #} - {# (x \oplus y)' = (xy'+x'y)' = (x'+y)(x+y') = xy+x'y' #} ㅇ XNOR 게이트 IC 例) 74266 등 3. XOR,XNOR 진리표(Truth Table)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]