Cross Product, Vector Product, Outer Product 크로스 곱, 외 적, 외 곱, 벡터 적(積), 벡터 곱 | (2020-08-09) |
▷
Top
▷
기초과학
▷
수학
▷
대수학
▷
선형 대수학
▷
벡터
▷
벡터의 크기,각도,거리,직교,투영
1. 외적/외곱/벡터적/벡터곱 (Cross Product,Vector Product,Outer Product) ㅇ 임의 두 벡터로부터 또다른 벡터량을 생성해내는 연산 - 스칼라적과는 달리, 그 결과가 스칼라가 아닌 또다른 벡터량이 됨 . 3 차원 공간의 벡터에서 만 적용 가능함 2. 외적의 정의 ㅇ u x v = ∥u∥∥v∥ sin θ n = w - 크기(길이) : A,B에 의해 만들어진 평면 면적 ∥w∥ = ∥u∥∥v∥ sin θ . 두 벡터를 인접시킨 평행사변형의 넓이와 같음 . θ : u, v의 사잇각 - 방향 : 그 평면에 수직인 법선 방향 ☞ 오른손 법칙 ㅇ 외적의 도형 표현ㅇ 외적의 행렬 표현
ㅇ 외적의 방향
3. 외적의 성질 ㅇ 교환법칙이 성립하지 않음 -
ㅇ 결합법칙이 성립하지 않음 -
ㅇ 분배법칙이 성립함 -
ㅇ 스칼라배 -
ㅇ 영벡터 -
4. 내적,외적의 관계식 ㅇ 직교성 (uxv는 u,v와 직교함)
ㅇ 라그랑주 항등식
ㅇ 내적과 외적과의 관계
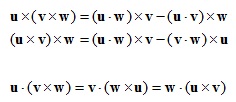
▷벡터의 크기,각도,거리,직교,투영
1. 내적 2. 크기(노름) 3. 거리 4. 직교 5. 외적 6. 투영 7. 슈바르츠 부등식 8. 피타고라스 정리