Cyclic Code, Cyclic Coding 순회 부호, 순환 부호 | (2023-12-29) |
Linear Cyclic Block Code, 선형 순회 블록 코드, 선형 순회 블록 부호 | |
▷
Top
▷
방송/멀티미디어/정보이론
▷
정보이론/코딩
▷
채널부호화
▷
블록 부호
▷
순회 부호
1. 순회 부호 (Cyclic Code) ㅇ 선형 블록 부호 (선형 부호)의 일종 - 즉, 선형 블록 부호의 부분집합 임 . 선형성에 순회성 (순환성 : 무한 반복/되풀이)이 추가적으로 부과됨 ㅇ 주요 특징 - 잘 정의된 수학적 구조 - 부호화,복호화의 용이성 등 ※ 1957년 Eugene Prange가, - 순회 블록 부호의 수학적 기초를 세운 이후, - 선형 블록부호 대부분이 순회 부호를 사용 2. 순회부호의 조건 ㅇ (선형성) 선형부호 일 것 즉, 두 부호어의 합이 그 부호에 속하는 다른 유효 부호어가 됨 ㅇ (순환성) 임의의 한 부호어를 순환 이동(Cyclic Shift)시키어도 이 역시 유효 부호어일 것 ※ 순회부호 例) C = {0000,1010,0101,1111} - 선형성 검토 . (중첩의 원리) 그 어떤 두 부호어의 합도 모두 C에 속하므로 C은 선형부호임 .. 1010 ⊕ 1111 = 0101, 1010 ⊕ 0101 = 1111, 1111 ⊕ 1111 = 0000, ... 등 - 순환성 검토 . (0000)->(0000), (1010)->(0101)->(1010), (1111)->(1111) * (0...0), (1...1) 처럼, 모두 `0`, 모두 `1`인 부호어는, 항상 포함됨 ㅇ 순회부호 실제 例 - 순회 해밍 부호, 순회 Golay 부호, BCH 부호, RS 부호, CRC, PN 코드 등 3. 순회부호의 특징 ㅇ 효율적인 부호화/복호화 가능 - 수학적으로 간결한 표현 * 특히, 순회 부호는 유한체(Galois Field) 이론에 크게 의존 함 . 순회부호에 대해, 갈로아 유한체(Galois Finite Field) 행렬 표현에 의해, . 아주 단순하고도 효율적인 부호화/복호화 알고리즘을 도모할 수 있음 . 또한, 갈로아 유한체 이론은 효율적인 알고리즘 설계에 특히 유용함 ㅇ 따라서, 매우 간단하고 저렴한 전자회로로 쉽게 구현 가능 - 코드 그 자체가 구조적이고 규칙성을 갖으므로, 설계구현 용이 . 부호화 및 신드롬 계산이 간단한 시프트 레지스터를 이용하여 쉽게 구현 가능 .. 즉, 직렬 구현도 가능 ㅇ 주로, 오류제어 기능 위주 보다는, 구현이 간단하여 오류검출 용도로 더 폭넓게 쓰임 - 다중 비트오류에 대한 오류정정도 가능 4. 순회부호의 표현 및 생성 ☞ 부호 다항식 표현, 생성 다항식 참조 ㅇ `선형 블록부호`의 표현/생성은, - 주로, 부호 벡터 (부호어 표현), 생성 행렬 (부호어 생성 : 부호화)에 의해 가능하나, ㅇ `순회 부호`의 표현/생성은, - 주로, 부호 다항식 (부호어 표현), 생성 다항식 (부호어 생성 : 부호화)에 의함 ※ 부호 다항식 표현 例) q진 (n,k) 순회 부호는, - (n-k) 차수의 다항식에 의해 다음과 같이 표현 가능[# \mathbf{g}(X) = g_0 + g_1X + g_2X^2 + \cdots + g_{n-k-1}X^{n-k-1} + X^{n-k} #]. 단, {#g_0 \neq 0#}, {#g_i \in GF(q)#} ({#GF(q)#} : q개 원소를 갖는 유한체) . 한편, 2진(q=2)의 경우 : {#g_i#} = {0,1}, 3진(q=3)의 경우 : {#g_i#} = {0,1,2} 5. 순회부호의 구현 ㅇ 순회부호는 시프트 레지스터(LFSR)에 의해 쉽게 구현 가능함 ㅇ 선형 피드백 시프트레지스터(LFSR)에 의한 순회부호 회로구현 例)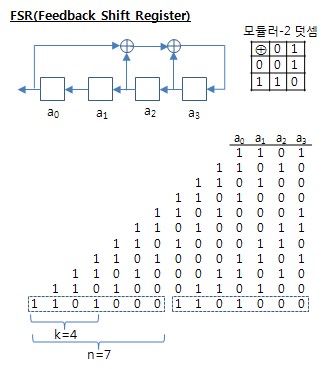
▷순회 부호
1. 순회 부호 2. 부호 다항식 3. 생성 다항식 4. CRC(순환중복검사) 5. CRC 생성 다항식 종류 6. BCH 부호 7. RS 부호 8. PN 코드 9. 최장 수열