Digital Frequency   디지털 주파수, 디지털 라디안 주파수

1. 디지털 주파수 이란?

  ㅇ 연속적인 주파수가 아니라, 이산적이고 샘플링된 주파수
     - 디지털 주파수는, 이산 주기신호를 주파수영역에서 표현할 때 필요한 개념
        . 이산 주기신호 例 : 이산 복소지수 신호 (ejΩn), 
                             이산 정현파 신호 (cos(Ωn),sin(Ωn))

  ㅇ 디지털 주파수 (Digital Frequency) : 정규화/규격화 주파수 (Normalized Frequency)
     - 
[# F = \frac{f}{f_s} #]
  [cycles/sample] 
        . 아날로그 주파수에 취한 샘플 주파수(f)들을 샘플링률(fs)로 나눈 값
           .. 즉, 샘플 주파수의 주기를 1로 규격화시킨 주파수
     - 값 범위 : 0 ≤ F ≤ 1

     * 한편, 디지털 주파수 F가, 
        . 주기적이려면, 반드시 `유리수`이어야 함   ☞ 아래 2.항 참조
        . 즉, F = k/N (k,N : 정수, F : 유리수)

  ※ [참고] 아날로그계,디지털계 간 비교      ☞ 푸리에변환의 시간 및 주파수 관계 참조
     - 아날로그 : 시간 t (seconds), 시간 주기 T, 주파수 f (cycles/second), 주파수의 주기 없음
     - 디지털   : 샘플 n (samples), 시간 주기 N, 주파수 F (cycles/sample), 주파수의 주기 : 1

  ㅇ 디지털 기본주파수 :  F0 = 1/N
     - F = kF0 = k/N 

  ㅇ 디지털 라디안 주파수 / 디지털 각 주파수 (Digital Radian Frequency/Angular Frequency)
     -  [rad/sample] 또는 Ω = 2πk/N
        . 디지털 주파수를 라디안 단위로 표현한 값
     - 값 범위 : 0 ≤ Ω ≤ 2π

  ㅇ 디지털 라디안 기본주파수 :  Ω0 = 2π/N


2. 디지털 주파수는 `유리수`이어야 => `주기`적이 됨

  ㅇ 연속 정현파는 항상 주기적이지만, 이산 정현파는 반드시 그렇지 않음
     - 연속 정현 신호 : 모든 아날로그 주파수에서, 저마다 고유(unique)하고, 주기성(periodic)을 보임
     - 이산 정현 신호 : 디지털 주파수가 주기적이려면, 유리수이어야 만 됨

   

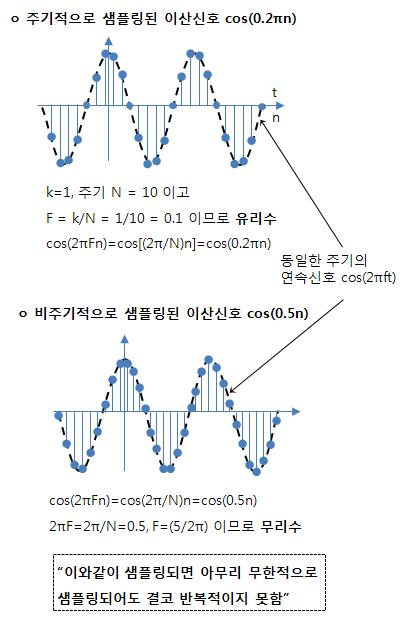
  ㅇ 결국,
     - 이산 정현파는 디지털 주파수가 유리수일 때 만 주기적이 될 수 있음
     - 모든 이산 정현파는 -π≤Ω≤π(-0.5≤F≤0.5)에서 표현 가능
        . 즉, 아날로그 주파수는 0 ~ ∞ 까지 가능, 
              디지털 주파수는 0 ~ π/T 에서 만 변화
     - 만일, 이산 정현파가 2π의 정수배 만큼 차이가 난다면 같은 신호임


3. 연속신호에 대한 주기적 샘플링 및 비주기적 샘플링 비교