Analytic Signal, Pre-Envelope, Causal Signal 해석적 신호, 인과적 신호 | (2025-07-03) |
▷
Top
▷
신호/시스템
▷
변환 해석
▷
푸리에 변환
▷
푸리에 변환 성질
1. 해석적 신호 (Analytic Signal, Pre Envelope) ㅇ 실수 신호 x(t)를 복소수 신호로 확장한 특별한 형태로, - 주파수 영역에서 양(positive) 주파수 성분만을 갖는 신호를 말함 - 즉, 푸리에 변환 X(ω) 관점에서 보면, . ω > 0 (양의 주파수)에서는, 원래 신호의 스펙트럼을 그대로 포함하고, . ω < 0 (음의 주파수)에서는, 값이 0이 되는, 복소수 신호 임 ㅇ 해석적 신호의 수식 표현[# x_a(t) = x(t) + j \, \hat x(t) \\ X_a(ω) = X(ω) + j \, \hat X(ω) = X(ω) + j \, (- j \, \text{sgn} \, ω) X(ω) #]- xa(t) : 실수값 신호 x(t)에 상응하는, 해석적 신호 (complex-valued) . 단지 양(positive)의 주파수에서 만 0 이 아닌 값을 갖는, 복소수값 신호 - x(t) : 원래의, 실수값 신호 (real-valued signal) . 항상 f = 0 을 중심으로 우대칭인 주파수 스펙트럼을 갖게되는, 실수값 신호 - x^(t) : x(t)의 힐버트 변환된 신호 . 힐버트 변환된 신호 : 모든 주파수 성분에 대해 90˚(π/2) 위상 지연시킨 신호 - X^(ω) : 힐버트 변환된 신호 x^(t)의 푸리에 변환 - sgn(ω) : 부호 함수 (Signum function) ㅇ 결과적으로, - 해석적 신호는, 실수 신호를 복소수 신호로 확장한 것으로, . 시간 영역과 주파수 영역에서 모두 유용한 해석적 성질을 제공함 - 특히, . 진폭과 위상을 분리하여 표현하기에 용이함 . 통신에서, 복소 기저대역 표현에 널리 사용됨 . 원 신호의 물리적 성질을 잃지 않으면서, 주파수 분석을 더 단순하게 만듬 2. 인과적 신호 (Causal Signal) ㅇ 푸리에변환 관계(주파수 스펙트럼)에서 볼 때, - `실수부 : 우대칭, 허수부 : 기대칭` 인 `복소수 신호` ㅇ 수식 표현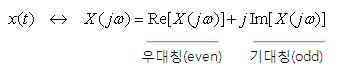
▷푸리에 변환 성질
1. 푸리에 변환의 성질 2. 푸리에 변환의 시간 주파수 관계 3. 푸리에 변환 쌍 4. 해석적, 인과적 신호 5. Dirichlet 조건 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]