Power Series Formula, Power Series Expansion 멱급수 공식, 멱급수 전개, 멱급수 근사 | (2020-02-06) |
로그함수 급수 | |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
수열,급수
▷
멱급수
1. 주요 멱급수 전개 (Power Series Expansion) ㅇ 테일러 급수ㅇ 매클로린 급수
ㅇ 삼각함수 급수
ㅇ 삼각 급수(Trigonometric Series)
[# a_0 + \sum^{\infty}_{n=1} (an \cos nx + b_n \sin nx) #]- 또는, 오일러 공식({# e^{j \theta} = \cos \theta + j \sin \theta #})에 의한 다음의 멱급수도 삼각 급수라고 함[# \sum^{\infty}_{n=-\infty} c_n e^{jnx} #]ㅇ 로그함수 급수 (메르카토르 급수, Mercator Series)[# \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} + \cdots = \sum^{\infty}_{n=1} \frac{(-1)^{n+1}x^n}{n} \quad\quad (-1 \leq x \leq 1)#]ㅇ 지수함수, 복소지수함수 급수ㅇ 이항 급수 (이항 정리)
ㅇ 분수 급수
2. 멱급수 근사식
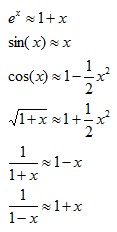
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]