Vector Differential Operator 벡터 미분 연산자 | (2024-07-08) |
Dell Operator, 델 연산자, Nabla Operator, 나블라 연산자 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학 (미적분 등)
▷
벡터해석학
▷
스칼라장,벡터장 연산
1. 벡터 미분 연산자 (Vector Differential Operator) : ∇ ㅇ 벡터 미분 연산자는, 벡터의 편미분을 연산자 형태로 나타낸 것 - (표기) {# \nabla = (\partial/\partial x)\;\mathbf{a}_x + (\partial/\partial y)\;\mathbf{a}_y + (\partial/\partial z)\;\mathbf{a}_z #} . 그 자체로는 벡터라고 할 수 없는, 연산자 형태로써, . 이를 스칼라 함수에 적용하면, 그 결과가 벡터가 됨 - (명칭) ∇ : 델(Del) 또는 나블라(Nabla) - (응용) . 장(스칼라장,벡터장 : 다변수 함수)에 대한, 다양한 미분 연산을 하는데 쓰여짐 ※ 한편, 스칼라 미분연산자는, - Dx = d/dx, Dy = dy/dx 같은 형태를 말함 2. 장(스칼라장,벡터장 : 다변수 함수)에서, 델 연산자(∇)의 사용 例 ㅇ ∇Ψ = grad Ψ : 스칼라 Ψ의 기울기 연산(Gradient Operation) => grad 연산자 - (표기)[# ∇f = \text{grad}\ f = \frac{\partial f}{\partial \mathbf{x}} = \left( \frac{\partial f}{\partial x_1} \; \frac{\partial f}{\partial x_2} \; \cdots \; \frac{\partial f}{\partial x_n} \right) #]. 다변수함수,벡터,행렬을 미분하면, 그 결과가 벡터,행렬이 됨 - (명칭) . ∇f : 그래디언트(Gradient). 즉, 다변수 함수에 대한 벡터 미분 - (의미) . {#∇f#}는, 주어진 위치 {#(x_1,x_2,\cdots,x_n)#}에서 함수 값이 가장 커지는 방향으로의 벡터임 ㅇ ∇·A = div A : 벡터 A의 발산(Divergence) => div 연산자 ㅇ ∇×A = curl A : 벡터 A의 회전(Curl) => curl 연산자 ㅇ ∇2 Ψ = ∇·∇ Ψ = div grad Ψ : 스칼라 Ψ의 Laplacian => laplacian 연산자 3. 좌표계별 델 연산자 ㅇ 직각 좌표계ㅇ 원통 좌표계
ㅇ 구 좌표계
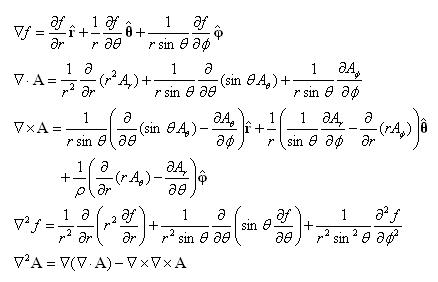
▷스칼라장,벡터장 연산
1. 장(Field) 2. 델 연산자 3. 기울기 연산 (grad) 4. 기울기 벡터장 5. 발산 연산 (div) 6. 회전 연산 (curl) 7. 라플라시안 (div grad) 8. 텐서 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]