Divergence 발산, 발산 연산자 | (2022-09-19) |
벡터의 발산, 다이버젼스, 다이버전스, div 연산자 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분적분
▷
극한,연속,발산
▷ Top ▷ 기초과학 ▷ 수학 ▷ 벡터해석학 ▷ 대수학 ▷ 선형 대수학 ▷ 벡터 ▷ 스칼라장,벡터장 연산
▷ Top ▷ 기초과학 ▷ 수학 ▷ 벡터해석학 ▷ 대수학 ▷ 선형 대수학 ▷ 벡터 ▷ 스칼라장,벡터장 연산
1. 발산 (Divergence) ㅇ 함수/수열/급수/적분 등이, `극한 (Limit)`으로 `수렴 (Convergence)`하지 않음 - 양의 무한대, 음의 무한대 :[# \lim_{x \to a} = \pm ~ \infty #]- 요동하는 등 2. [벡터장] 벡터의 발산 연산자 (Divergence, ∇·) ㅇ 의미 - 벡터 미적분에 나오는 벡터 연산자 중의 하나 - 계의 한 점에서 벡터 장이 퍼져 나오는지, 아니면 모여서 없어지는지의 정도를 보여줌 ㅇ 표현식[# \text{div} ~ \mathbf{A} = \nabla \cdot \mathbf{A} = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} \\ \quad\quad\; = \lim_{\Delta \text{V} \to 0} \frac{\oint_S \mathbf{A} \cdot d \mathbf{S}}{\Delta \text{V} } #]ㅇ 특징 - 벡터 곱셈으로 얻어지며, - 그 결과는 항상 스칼라장이 됨 ㅇ 부호 * 어떤 벡터장에 대한 발산 연산자(∇·) 취한 값이, - 양수(+)이면, 장(場)의 발산(divergence) - 음수(-)이면, 장의 수렴/흡수/소멸(sink) - 영(0)이면, 장의 변화 없음 (즉, 원천/소스가 존재하지 않음) ※ [참고] - 벡터 미분 연산자 : 발산 연산자(div), 기울기 연산자(grad), 회전 연산자(curl) - 관련 정리,법칙 : 발산 정리, 가우스 법칙 등 참조 3. [벡터장] 좌표계에 따른 발산 연산의 표현식 ㅇ 직각좌표계ㅇ 원통좌표계
ㅇ 구좌표계
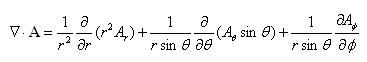
▷극한,연속,발산
1. 극한,연속 2. 발산 3. 중간값 정리
▷스칼라장,벡터장 연산
1. 장(Field) 2. 델 연산자 3. 기울기 연산 (grad) 4. 기울기 벡터장 5. 발산 연산 (div) 6. 회전 연산 (curl) 7. 라플라시안 (div grad) 8. 텐서