Log Normal Distribution 로그 정규분포, 로그 노말 분포, 대수 정규분포 | (2022-02-13) |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 모형,분포
▷
정규분포
▷ Top ▷ 통신/네트워킹 ▷ 무선/이동통신 ▷ 무선 전파 ▷ 전파 모델 ▷ 소규모 전파모델 ▷ 페이딩 확률해석
▷ Top ▷ 통신/네트워킹 ▷ 무선/이동통신 ▷ 무선 전파 ▷ 전파 모델 ▷ 소규모 전파모델 ▷ 페이딩 확률해석
1. 로그 정규분포 ㅇ 로그 정규분포를 갖는 확률변수(X)에 로그를 취한 확률변수(Y = In(X))가 정규분포를 따름 - 즉, Y = In(X) ~ N( In(x); μY,σY ) ㅇ 또는, 정규분포 확률변수(Y)에 지수를 취한 확률변수(X = eY)가 로그 정규분포를 따름 - 즉, X = eY ~ LN( x; μX,σX ) ※ [참고] 지수함수,로그함수는 서로 역함수 관계에 있음 2. 로그 정규분포 형태ㅇ 중심 그 자체에는 분포 없고, 중심 부근에서 큰 분포를 갖으며, - 중심에서 멀어질수록, 점진적으로 감소하는 긴꼬리 형태의 분포 ㅇ 즉, 점진적으로 감소하는 긴 우측꼬리를 갖는 확률분포 형태 - 큰 값들이 왼쪽에 많아 약간 왼쪽으로 기울어진(Skewed,왜도를 갖는) 확률분포 ㅇ 특히, - 확률변수 X = eY는 비대칭적 확률분포이나, - 확률변수 Y = ln(X)는 대칭적 정규분포를 따름 * 로그 정규분포는 정규분포로부터 유도될 수 있음 3. 로그 정규분포 특징 ㅇ 표기 : X ~ LN(μX,σX) - 단, X = eY, Y ~ N(μY,σY) ㅇ 확률밀도함수(PDF)
ㅇ 누적분포함수(CDF)
ㅇ 기대값(Expected Value)
ㅇ 분산(Variance)
ㅇ 백분위수 - 100(1-α)% 백분위수 : xα
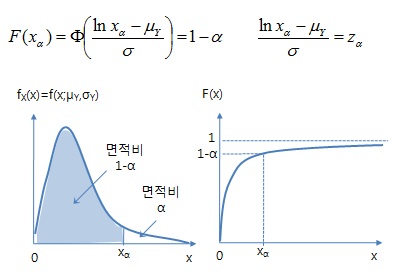
▷정규분포
1. 정규분포 2. 로그 정규분포 3. 이변량 정규분포
▷페이딩 확률해석
1. 로그 정규 확률분포 2. 레일레이 페이딩 3. 레일레이 확률분포 4. 라이시안 확률분포