Gauss Elimination Method, Back Substitution   가우스 소거법, Gauss 소거법, 후진대입법, 가우스 조르단 소거법

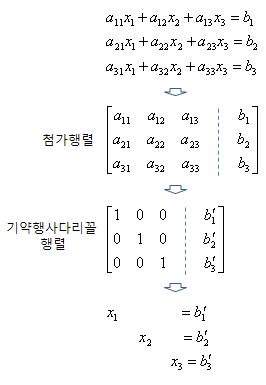
1. 일차 연립방정식의 일반적인 풀이법

  ㅇ 대입법 (Method of substitution)
     - 특정 미지수를 다른 미지수들에 의한 식으로 표현하여, 이를 다른 식에 대입하여 푸는 방법

  ㅇ 가감법 (Method of elimination by adding and subtracting)
     - 한 식에 상수 또는 식을 곱한 후, 다른 식과 더하거나 빼어서,
     - 더 풀기 쉬운 형태의 연립방정식으로 만들어 푸는 방법
     - 경우에 따라, 미지수가 많으면, 되풀이 하여, 미지수 수가 1개가 되도록 유도함

  ㅇ 소거법 (Elimination Method)
     - 통상, 연립방정식에서, 미지수 문자를 하나씩 소거해가는 방법을 총칭함

     - 주로, 아래의 세가지 연산을 이용하면서, 주어진 연립방정식을 변형시켜,     ☞ 기본 행렬 연산
       동일한 해집합을 갖는 풀기쉬운 연립방정식으로 변환해 나가는 방법을 말함 
        ① 두 방정식의 교환
        ② 한 방정식에 0이 아닌 상수를 곱함
        ③ 한 방정식에 임의의 상수를 곱하여 다른 방정식에 더함
 

2. 가우스 소거법 (Gauss Elimination Method)

  ㅇ 선형 연립방정식의 해를 구하는 가장 표준적인 방법

     - 선형 연립방정식의 첨가행렬을,
     - 기본행연산에 의해, 행줄임(즉,소거,Elimination)함으로써,
     - 점차적으로, 상 삼각행렬로 바꾸고, (즉, 행사다리꼴 행렬로 변환시키고,)
     - 후치환(Back Substitution,후진대입법)에 의해, 해를 구하는 체계적인 과정
     - (결국, 소거법을, 기본행연산에 의해, 행렬로 표현 가능)

  ㅇ 크게, 두 단계로 구성됨
     ① 전진 소거 (forward elimination)
     ② 후진 대입 (back substitution)
     


3. 가우스-요르단 소거법 (Gauss-Jordan Method)

  ㅇ 가우스 소거법의 변형
     - 첨가 행렬로부터 기약 행 사다리꼴로 변환시킴