근궤적 작도법, 근궤적 개략 그리기 | (2020-10-16) |
▷
Top
▷
전기전자공학
▷
자동제어
▷
근궤적 기법
1. 근궤적 성질 및 개략 그리기 (작도법 규칙) ※ K가 0 ~ +∞ 로 변할 때, G(s)H(s) = -1/K 를 만족하며 근이 그리는 궤적 ㅇ 근궤적의 출발점 (K=0 : 극점) - 출발점 K=0 에서, 개루프전달함수 G(s)H(s)가 극점에 접근 ㅇ 근궤적의 종착점 (K=∞ : 영점 또는 무한대) - 종착점 K=∞ 에서, 개루프전달함수 G(s)H(s)가 영점 또는 무한대에 접근 . 여기서, 무한대는 극점 개수가 영점 개수 보다 많은 경우에 한 함 ㅇ 근궤적의 가지수 = 특성방정식의 차수 - 근궤적 수는 폐루프 전달함수의 극점 수(특성방정식의 근 수)와 같음 . 즉, 특성방정식의 차수 만큼의 근궤적이 존재함 * K가 0 ~ +∞ 변할 때의 각 근이 취하는 궤적으로써, 결국 근의 수와 같음 ㅇ 근궤적이 실수축에 대해 대칭적임 - 물리적 구현 가능 시스템이려면, 특성방정식 근[수학]이 실근 또는 복소 공액근 이어야 함 ㅇ 실수축 상의 근궤적 존재 유무 - 실수축을 실수 극점,영점으로 분할할 때, - 실수축 임의 점의 오른쪽에 극점 및 영점을 합한 수가 - 홀수개이면, 그 영역에 근궤적이 존재하고, 짝수개이면, 그 영역에 근궤적이 존재 않음 ㅇ 이득 K가 무한 커지면 근궤적이 접근하는 점근선에 대한 특성 - 점근선의 갯수 = G(s)H(s)의 극점 개수 - G(s)H(s)의 영점 개수 = n - m - 점근선의 실수축과의 교차점 . 점근선의 교차점 = (-∑pi + ∑zi)/(n - m) = (G(s)H(s)의 모든 극점들의 합 - G(s)H(s)의 모든 영점들의 합)/ (극점의 개수 - 영점의 개수) - 점근선의 실수축과의 각도 . Φk = (2k + 1)180˚/(n - m) | k = 0,1,...,n-m-1 ㅇ 기타 성질 - 무한대에서의 동작 특성 - 근궤적 분기점 - 근궤적과 허수축과의 교차점 2. 근궤적 작도 例)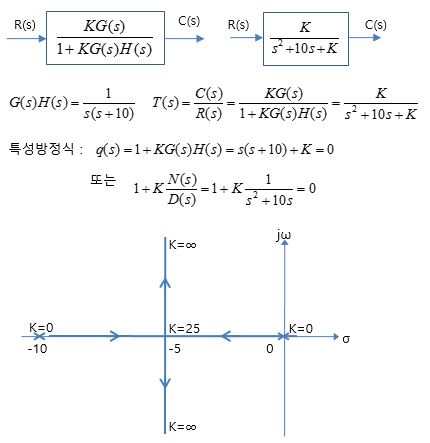
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]