PSD Power Spectral Density, Power Spectrum Density 전력 스펙트럼 밀도 | (2023-06-10) |
전력밀도 스펙트럼, 전력 스펙트럼 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
신호 표현/성질
▷
신호 에너지/신호 전력
▷
스펙트럼 밀도
▷ Top ▷ 통신/네트워킹 ▷ 통신이론 ▷ 디지털 통신 ▷ 기저대역 디지털통신 ▷ 선로 부호화 ▷ 선로부호 전력스펙트럼
▷ Top ▷ 통신/네트워킹 ▷ 통신이론 ▷ 디지털 통신 ▷ 기저대역 디지털통신 ▷ 선로 부호화 ▷ 선로부호 전력스펙트럼
1. 전력 스펙트럼 밀도 (Power Spectrum Density, PSD) ㅇ 주파수 스펙트럼(주파수 영역) 상의 전력 표현 - 신호 주파수에 따른 전력 밀도의 분포 ☞ 밀도, 전력밀도, 스펙트럼밀도 참조 ※ (밀도 단위의 표현 방식) - 단위 주파수 당 전력, 단위 대역폭 당 전력이면, [Watt/Hz], [W/Hz] . 만일, 굳이 전압,전류도 스펙트럼 밀도로 표시코자 한다면, .. 전압신호이면 [V2/Hz], 전류신호이면 [A2/Hz] 2. 전력 스펙트럼 밀도의 중요성/사용이유 ㅇ 통신 신호의 `전력스펙트럼밀도(PSD)` 분포 정보를 알면, - 전송,변조 등에서 주파수에 따른 `파형 형태를 어떻게 정할지`를 알 수 있음 - 왜곡 없이 전송 가능한 `소요 대역폭, 대역 효율성`을 알 수 있음 - 통신 시스템 설계시 `소요 대역폭 요구에 대한 예측` 가능 등 ㅇ 또한, 전력스펙트럼밀도에 의해, 주파수영역에서 신호를 취급하다 보면, - 랜덤신호에서도 마치 결정신호 처럼 유사하게 적용 가능 3. 전력 스펙트럼 밀도의 정의 ㅇ 결정신호(전력신호)ㅇ 랜덤과정
- 자기상관 및 전력스펙트럼은 푸리에 변환 쌍 관계가 있음 => 위너 킨친 정리 4. 랜덤과정에 대한 전력 스펙트럼 분포 ㅇ 랜덤과정에서 푸리에변환은 정확하게 정의하기가 어려움 - 랜덤과정 내 랜덤신호(표본함수)의 푸리에변환은 그때마다 다르므로 정확히 정의 못함 - 또한, . 비정상상태과정은, 주파수 전력에 대해 정의할 수 없음 . 오직 정상상태과정(WSS) 만, 통계적 기대값으로 주파수 전력에 대해 정의 가능 ㅇ 정상상태과정(WSS) 하의 랜덤과정은, 평균적 개념에 의한 묘사가 가능 - 즉, `자기 상관`, `교차 상관`, `자기 공분산`과 같은 평균적 개념들을 사용 가능 ㅇ 결국, 랜덤과정의 주파수에 따른 전력 정보를 얻으려면, - 랜덤과정의 자기상관함수의 푸리에변환이 전력스펙트럼밀도가 되므로, - 이를통해 랜덤과정의 주파수 스펙트럼 관련 유익한 정보를 얻게됨 . 즉, 자기상관 RX(τ)를 이용함으로써, 굳이 시간신호에 대한 푸리에변환을 할 필요 없이, . 전력스펙트럼 분포를 취급할 수 있게됨 - 정상상태과정 하의 랜덤과정 평균전력은,
5. 전력 스펙트럼 밀도의 수학적 성질 ㅇ 양(positive)의 함수 : Sx(f) ≥ 0 또는 SX(f) ≥ 0 ㅇ 우함수(우대칭,Even) : Sx(-f) = Sx(f) 또는 SX(-f) = SX(f) ㅇ x(t) 또는 X(t)가 실수 함수이면, 전력밀도스펙트럼도 실수 함수 ㅇ 주파수 전체 적분 = 평균전력
- 주파수 전체를 통해 전력스펙트럼밀도(PSD) Sx(f)를 적분하면 평균전력이 됨 6. 전력 스펙트럼 밀도의 입출력 및 변조 전후 ㅇ 선형시불변시스템 입출력
ㅇ 변조 전후
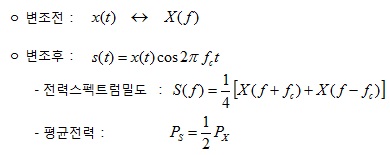
▷스펙트럼 밀도
1. 스펙트럼 밀도 2. ESD(에너지스펙트럼밀도) 3. PSD(전력스펙트럼밀도) 4. 파시발 정리,위너-킨친 정리
▷선로부호 전력스펙트럼
1. 전력 스펙트럼 밀도 2. 선로부호 PSD 3. 랜덤 진폭 자기상관 4. 주기적 랜덤 펄스 열 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]