FSK Orthogonality, FSK Correlation   FSK 직교 조건, FSK 상관성, FSK 상관계수

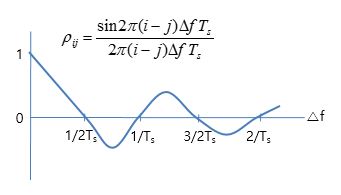
1. 직교 FSK 조건
 
  ㅇ FSK가 직교성을 갖으려면, 두 신호를 곱하여 적분한 결과가, `0` 이어야 함   ☞ 직교성 판단 참조
      
[# \int^{(k+1)T}_{kT} s_1(t)s_2(t) dt = 0 #]

  ㅇ 따라서, 
      
[# \int^{(k+1)T}_{kT} s_1(t)s_2(t) dt \\
          = \int^{(k+1)T}_{kT} \cos(2πf_1t+φ)\cos(2πf_2t+φ) dt \\
          = \frac{1}{2}\int^{(k+1)T}_{kT}[cos(2π(f_1+f_2)t+2φ)+ cos(2π(f_1-f_2)t)]dt \\
   = \left. \frac{1}{4π(f_1+f_2)}[\cos(2φ)\sin(2π(f_1+f_2)t+2φ)+\sin(2φ)\cos(2π(f_1+f_2)t)] \right|^{(k+1)T}_{kT} \\ 
   \quad  + \left. \frac{1}{4π(f_1-f_2)}[\sin(2π(f_1-f_2)t)] \right|^{(k+1)T}_{kT} \\
   = 0 #]

  ㅇ 위 식이 성립하려면,
      
[# 2π(f_1+f_2)T = 2nπ, \quad 2π(f_1-f_2)T = mπ \\
         f_1 = \frac{2n+m}{4T}, \quad f_2 = \frac{2n-m}{4T} \\
         Δf = f_1-f_2 = \frac{m}{2T} \\
         f_c = \frac{f_1+f_2}{2} = \frac{n}{2T} #]

  ㅇ 결국, 직교성 유지 조건은,
     - 두 주파수(f1,f2)가, 각각 1/4T의 정수배
     - 주파수 차이(Δf)가, 1/2T의 정수배
     - 중심 주파수(fc)가, 1/2T의 정수배

  ㅇ 특히, 주파수 차이가 Δf = 1/T 이면,
     - 이를 Sunde FSK 이라고 함
        . 2개 심볼 주파수 간의 간격을 정확히 심볼률(R = 1/T)과 같게 한 것 (Δf = 1/T)

  ㅇ 한편, FSK 신호가, 연속적인 위상을 갖도록 하려면, 
     - 주파수 차이가 Δf = k/T (1/T의 정수배)이면 됨         ☞ CPFSK(Continuous Phase FSK) 참조


2. FSK 파형 상관성 = FSK 상관계수         ☞ 신호 상관계수 (Signal Correlation Coefficient) 참조

  ㅇ 두 FSK 신호 간의 유사성(Similarity)/차이점(Dissimilarity)에 대한 척도

     

  ㅇ 즉, 주파수 분리 Δf에 대한 함수로써 표현 가능

  ㅇ 결국, 이를 통해, 직교성을 쉽게 판단 가능
     - 만일, Δf가 1/2Ts의 배수일 때 신호 파형 간에 직교함 (ρij = 0)
     

1. ▷ Top (분류 펼침)      :     1,591개 분류    6,514건 해설 검색 펼침