Chain Rule 연쇄 법칙 | (2024-04-18) |
합성함수의 미분법 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학 (미적분 등)
▷
미분적분
▷
미분
▷
미분 공식/정리/법칙
1. 연쇄 법칙 (Chain Rule) ㅇ 두 함수를 합성한 합성함수의 미분법 - "합성함수 f ∘ g 의 도함수는, f,g 각각의 도함수들의 곱과 같음" - "합성함수의 변화율은, 각 함수의 변화율들의 곱과 같음" ㅇ 즉, - F = f ∘ g, F(x) = f(g(x)) 일 때, => F'(x) = f'(g(x))·g'(x) - y = f(u), u = g(x) 일 때, => dy/dx = dy/du du/dx 2. 일변수,이변수,삼변수,일반함수의 연쇄 법칙 ㅇ 일변수함수의 연쇄법칙[# \frac{du}{dx} = \frac{du}{dt} \frac{dt}{dx} #]ㅇ 이변수함수의 연쇄법칙ㅇ 삼변수함수의 연쇄법칙
ㅇ 일반 함수의 연쇄법칙 - u는 n개의 변수 x1,x2,...,xn의 미분가능한 함수이고, - 각 xj는 m개의 변수 t1,t2,...,tm의 미분가능한 함수일 때,
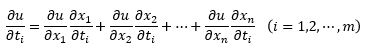
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]