Sine Rule, Law of Sines, Cosine Law   사인 법칙, Sine 법칙, 정현 법칙, 사인 정리, 코사인 법칙, Cosine 법칙, 여현 법칙, 코사인 정리

1. 사인 법칙 (Sine Rule)

  ㅇ 삼각형 변의 길이와 끼인 각의 관계
     - 삼각형의 세 각의 사인함수와 변의 길이와의 관계를 보여주는 법칙

  ㅇ 삼각형 변의 길이는 대각의 Sine 값에 비례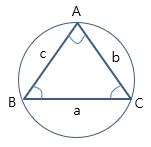
       
       
[# \frac{a}{\sin A} = \frac{b}{\sin B} \frac{c}{\sin C} = 2R #]
     - (R : 외접원의 반지름)


2. 코사인 법칙

  ㅇ 삼각형 내각과 그 대변의 길이와의 관계
       
       
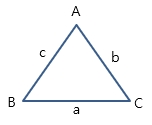[# a^2 = b^2 + c^2 - 2bc\cos A \\ 
   a^2 = b^2 + c^2 - 2ac\cos B \\
   c^2 = a^2 + b^2 - 2ab\cos C #]

  ㅇ 삼각형의 두 변과 그 사이에 끼인 각을 알면, 나머지 변을 구할 때 유용