Circuit Impedance   회로 임피던스

1. 회로 임피던스 (Circuit Impedance)

  ㅇ 일반 회로에서, 정현파 주파수 변화에 따라, 전압,전류 비(比)의 함수적 관계로 반응
     - 저항(抵抗) 속성인 전압,전류의 比에 대한 주파수에 따른 복합효과


2. 회로 소자별 주파수에 따른 임피던스 특성

  ㅇ 저항 
     - (주파수 변화에 무관/일정)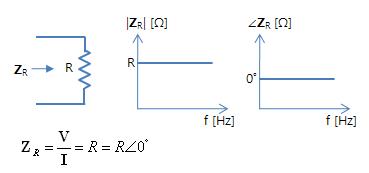

        
          
[# \mathbf{Z}_R = \frac{\mathbf{V}}{\mathbf{I}} = R = R \angle 0˚#]
 

  ㅇ 인덕터
     - (주파수가 커짐에 따라 커짐. 고주파수에서 영향 우세)

        
          
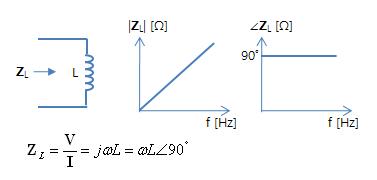[# \mathbf{Z}_L = \frac{\mathbf{V}}{\mathbf{I}} = jωL = ωL \angle 90˚#]
 

  ㅇ 커패시터
     - (주파수가 감소하면 커짐. 저주파수에서 영향 우세) 

        
          
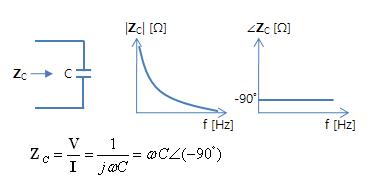[# \mathbf{Z}_C = \frac{\mathbf{V}}{\mathbf{I}} = \frac{1}{jωC} = \frac{-j}{ωC}
                          = ωC \angle (-90˚)#]
 

  ※ 저주파계(통상의 전자회로)에서는,
     - R, C 특성 만을 고려하여 회로 설계를 취급함


3. 회로 임피던스의 위상

  ㅇ 만일 일반적인 전송 케이블에 교류 전압을 인가하였을 경우에,
     - 전기 저항(R)과 누설 콘덕턴스(G)에는, 전압과 동일한 위상의 전류가 흐르고,
     - 인덕터에(L)는, 전압 보다 90˚ 느린 전류가 흐르고,
     - 커패시터(C)에는, 전압 보다 90˚ 빠른 전류가 흐르게 됨.


4. 직렬 RLC 회로에서의 임피던스

    
       
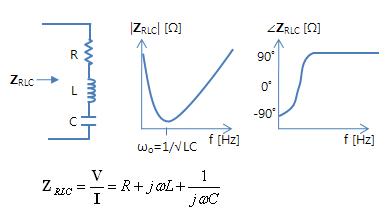[# \mathbf{Z}_{RLC} = \frac{\mathbf{V}}{\mathbf{I}} = R + jωL + \frac{1}{jωC} #]
 


5. 참고용어

  ㅇ 임피던스의 정의                     =>  임피이던스(Impedance)
  ㅇ 전송 선로 상에서                    =>  특성 임피던스 (Charaterictic Impedance)
  ㅇ 전자기파 매질 특성에 따른 임피던스  =>  고유 임피던스(Intrinsic Impedance) 
  ㅇ 자유공간 상에서                     =>  전파 임피던스 (Wave Impedance)