Spectrum Density, Density Spectrum 스펙트럼 밀도, 밀도 스펙트럼 | (2025-10-10) |
Spectral Density | |
▷
Top
▷
신호/시스템
▷
신호 표현/성질/종류
▷
신호 에너지/신호 전력
▷
스펙트럼 밀도
1. 스펙트럼 밀도 (Spectrum Density) ㅇ 신호의 주파수 영역 상에서, 에너지,전력 등의 밀도 분포 ☞ 밀도(Density) 참조 - 단위 스펙트럼(대역폭) 당 에너지의 크기 [J/Hz] : (에너지 스펙트럼 밀도) - 단위 스펙트럼(대역폭) 당 전력의 크기 [W/Hz] : (전력 스펙트럼 밀도) . `스펙트럼 상의 전력밀도`,`공간 상의 전력 밀도` 구분은, ☞ 전력 밀도(Power Density) 참조 ㅇ 주요 용도 : 통신 대역폭 평가, 필터 및 시스템 응답 특성 평가, 신호 간 간섭 분석 등 2. (에너지, 전력, 전압) 스펙트럼 밀도 ㅇ 에너지 스펙트럼 밀도 [Joule/Hz, (Watt sec)/Hz] ☞ Energy Spectrum Density(ESD) 참조 - 주파수 함수로써의 에너지 분포 . 에너지 스펙트럼 밀도 곡선의 전체 면적(적분)은 `총 에너지`가 됨 .. 총 에너지 :[# E_{tot} = \int^{\infty}_{-\infty} |x(t)|^2 dt = \int^{\infty}_{-\infty} |X(f)|^2 df #].. 에너지 스펙트럼 밀도 :[# G(f) = |X(f)|^2 #]ㅇ 전력 스펙트럼 밀도 [Watt/Hz, J/sec/Hz] ☞ Power Spectrum Density(PSD) 참조 - 주파수 함수로써의 전력 분포 . 전력 스펙트럼 밀도 곡선의 전체 면적(적분)은 `평균 전력`이 됨 .. 평균 전력 :[# P_{avg} = \int^{\infty}_{-\infty} S(f) df = < x^2(t)> #].. 전력 스펙트럼 밀도 :[# S(f) #]ㅇ 또한, 주파수 함수로써의 전압 분포도 정의할 수 있음 - 전압 스펙트럼 밀도 (Voltage Spectrum Density,VSD) [Voltage/Hz, V/Hz][# V(ω) = \int^{\infty}_{-\infty} v(t) e^{-jωt} dt \longleftrightarrow v(t) = \frac{1}{2π} \int^{\infty}_{-\infty} V(ω)e^{jωt}dω #]※ 위에서, 전체 면적 이라함은 전 주파수 영역에 걸친 적분을 뜻함 3. 스펙트럼 밀도의 함수적 특징 ㅇ 주파수에 대해, 양의 값 (positive) ㅇ 주파수에 대해, 실수 (real) ㅇ 주파수에 대해, 우함수 (even) 4. 스펙트럼 밀도의 입출력 관계 (LTI 시스템 한)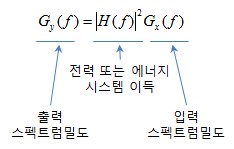
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]