Gauss Prabability Process, Gaussian Random Process 가우스 확률과정, 가우시안 랜덤과정 | (2023-11-21) |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 과정
▷
특별한 랜덤과정
1. 가우스 확률과정 ㅇ 어떠한 n개의 임의 시간 t1,t2,...,tn에서, 랜덤변수 X(t1),X(t2),...,X(tn)들이, 결합적 가우시안 분포(Jointly Gaussian)를 갖을 때, 이를 가우시안 확률과정이라고 함 2. 가우스 확률과정 특징 ㅇ 가우스 확률과정의 선형 연산은 또다른 가우스 확률과정이됨 ㅇ 2개 랜덤변수(X,Y)에 대한 결합 가우시안 확률밀도함수(PDF)[# f_{XY}(x,y) = \frac{1}{2π\,σ_Xσ_Y\sqrt{1-ρ^2}} \; \exp \left\{ -\frac{1}{2(1-ρ^2)} \left[ \left( \frac{x-μ_X}{σ_X} \right)^2 - \frac{2ρ(x-μ_X)(y-μ_Y)}{σ_Xσ_Y} + \left( \frac{y-μ_Y}{σ_Y} \right)^2 \right] \right\} #]- 여기서, μ : 기대값(평균), σ2 : 분산, ρ : 상관계수[# μ_X = E[X],\; μ_Y = E[Y],\; σ^2_X = E[(X-μ_X)^2],\; σ^2_Y = E[(Y-μ_Y)^2],\; ρ = E \left[ \frac{(X-μ_X)(Y-μ_Y)}{σ_Xσ_Y} \right] #]- [참고] 1개 랜덤변수(X)에 대한 단일 가우시안 확률밀도함수[# f_X(x) = \frac{1}{σ\sqrt{2π}}\;e^{-\frac{(x-μ)^2}{2\,σ^2}} #]ㅇ N개 랜덤변수에 대한 결합 가우시안 확률밀도함수(PDF)- `확률벡터의 기대값` 및 `확률벡터의 분산(공분산 행렬)`으로 완전하게 나타낼 수 있음 . 확률벡터의 기대값 = 평균 벡터(Mean Vector)
. 확률벡터의 분산 = 공분산 행렬(Covariance Matrix)
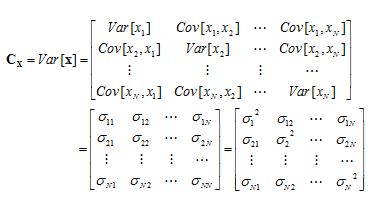
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]