Trigonometric Identities 삼각함수 공식, 삼각함수 항등식 | (2020-06-01) |
배각 공식, 반각 공식 | |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
기하학
▷
삼각법
▷
삼각함수,쌍곡선함수
1. 삼각함수 기초 공식, 정리 ㅇ 위상편이 - sin θ = cos (θ - π/2) 또는 sin (π/2 - θ) = cos θ . 사인함수는 코사인함수를 우측으로 90˚ 또는 π/2 라디안 만큼 편이시킨것 - sin (π - θ) = sin θ ㅇ 덧셈 정리[# \cos(α\pmβ) = \cosα\cosβ \mp \sinα\sinβ \\ \sin(α\pmβ) = \sinα\cosβ \pm \cosα\sinβ #]ㅇ 比 관계ㅇ 역수 관계
2. 피타고라스 정리 ※ ☞ 피타고라스 정리(Pythagorean Theorem) 참조 - 직각 삼각형의 세 변 사이의 특별한 관계를 방정식 형태로 나타낸 정리 3. 삼각함수의 (곱셈 → 덧셈),(덧셈 → 곱셈) 변환 정리 ㅇ 곱셈 → 덧셈 변환 정리 (product-to-sum)
[# \cosα\cosβ = \frac{1}{2}[\cos(α+β) + \cos(α-β)] \\ \sinα\sinβ = \frac{1}{2}[\cos(α-β) - \cos(α+β)] \\ \sinα\cosβ = \frac{1}{2}[\sin(α+β) + \sin(α-β)] #]ㅇ 덧셈 → 곱셈 변환 정리 (sum-to-product)4. 배각 공식, 반각 공식, 차수 줄이기 ㅇ 배각 공식 (double angle formula)
ㅇ 반각 공식 (half angle formula)
ㅇ 차수 줄이기 (power-reduction formula)
5. 두 삼각함수의 합
6. 삼각함수의 미분,적분
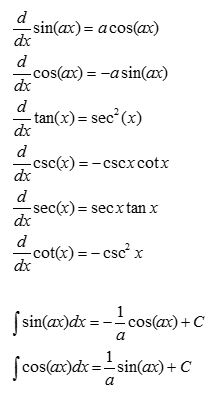
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]