Butterworth Filter, Butterworth Approximation 버터워스 필터, Butterworth 필터, Butterworth 근사 | (2024-09-12) |
Maximally Flat Approximation, 최대 평탄 근사 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
필터
▷
필터 근사 (Butterworth,Chebyshev등)
1. 다양한 필터 근사 구분 ㅇ Butterworth 필터 : 통과대역이 평평함, 스커트 특성(차단성)은 둔함 ㅇ Chebyshev 필터 : 통과대역에 만 Ripple 성분 있음, 스커트 특성은 날카로움 ㅇ Bessel 필터 : 저지대역에서 보다 완만한 롤 오프 (경사짐) 특성 ㅇ Elliptic 필터 : 통과대역 및 저지대역 모두에 Ripple (출렁임) 성분 있음2. Butterworth 필터 근사 (Filter Approximation) ㅇ 일반적인 필터 근사를 위한 기초 함수
[# |H(jω)| = \frac{K}{\sqrt{1+ε^2f(ω^2)}} #]ㅇ 버터워스 필터 근사 함수 ({# f(ω^2) = ω^{2n} #})[# |H(jω)| = \frac{K}{\sqrt{1+ε^2ω^{2n}}} #]ㅇ 정규화된 버터워스 필터 근사 함수 ({# K=1,ε=1,ω_c=1 #})[# |H(jω)| = \frac{1}{\sqrt{1+ω^{2n}}} #]3. Butterworth 필터함수의 특징 ㅇ 최대 평탄 특성 (maximally flat magnitude response) - 통과대역(Passband)이 편평한 반면에, 스커트 특성은 둔함- 한편, 비록 진폭응답은 편평(균등,균일)하지만, 위상응답은 비선형적 임 ㅇ 주파수가 커지면서, 단조 감소하는 함수 - (저주파) ω = 0 → 1 - (고주파) ω = ∞ → 0 ㅇ 필터 차수 n - n이 높을수록, 천이대역이 좁아지며 천이가 급격해짐 . 즉, 이상적인 필터에 가까워짐
ㅇ All Pole type (전 극점 형태) - 분모 다항식에 만 근이 있음 (all poles, no zeros) . 전달 함수에서, 영점(Zero) 없이 극점(Pole) 만을 포함하는 형태 ㅇ 모든 극점(Pole)이 단위원 상에 있음 ㅇ DC 이득 - |H(j0)| = 1 4. 버터워스 저역통과필터의 필터 차수별 전달함수 ㅇ H(s) = ±1/D(s)
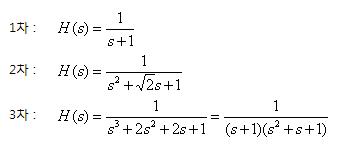
▷필터 근사 (Butterworth,Chebyshev등)
1. 필터 근사 2. 필터 함수 3. Butterworth 필터 4. Chebyshev 필터 5. Bessel 필터 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]