DTFT Discrete Time Fourier Transform 이산시간 푸리에 변환 | (2020-10-01) |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
이산 신호/이산 시스템
▷
이산 푸리에 표현
▷ Top ▷ 전기전자공학 ▷ 신호 및 시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에변환 표현 종류
▷ Top ▷ 전기전자공학 ▷ 신호 및 시스템 ▷ 변환 해석 ▷ 푸리에 변환 ▷ 푸리에변환 표현 종류
1. 이산시간 푸리에변환 (DTFT)ㅇ DTFT (이산시간 푸리에변환) - X(Ω) : `연속성` 및 `주기성`을 갖는 주파수 스펙트럼 (푸리에 계수) . 연속성 : 연속 실수 변수 Ω(디지털 라디안 주파수,[rad/sample])를 지수로 갖는 복소지수 연속 함수 임 . 주기성 : 주파수 구간 (0,2π) 또는 (-π,π)의 주기를 갖음 X(Ω+2πk)=X(Ω) .. 즉, 주파수가 유한한 범위 내에 있게 됨 ㅇ IDTFT (이산시간 역 푸리에변환) - x[n] : `이산성` 및 `비주기성`을 갖는 시간 신호 2. DTFT의 복소 좌표 표현 ㅇ DTFT X(Ω)는 복소수 연속함수 이므로, 다음과 같이 복소 좌표계로 표현 가능 - 직각좌표 형식 : {# X(Ω) = Re[X(Ω)] + jIm[X(Ω)] #} - 극좌표 형식 : {# X(Ω) = |X(Ω)| e^{j\angle X(Ω)} #} 3. DTFT의 성질 ㅇ 주기성 :
[# X(Ω+2mπ) = X(Ω) #]- 따라서, 전체 주파수영역을 굳이 모두 해석할 필요없이, 2π 구간 만 다루면 됨 ㅇ 대칭성 :[# X^*(Ω) = X(-Ω) #]☞ 공액 대칭 참조 - 따라서, 반주기 [0,π] 구간 만 해석해도 충분함 * 특히, 실수부 {#Re[X(Ω)]#}는 우 대칭, 허수부 {#Im[X(Ω)]#}는 기 대칭, 진폭스펙트럼 {#|X(Ω)|#}는 우 대칭, 위상스펙트럼 {#\angle X(Ω)#}는 기 대칭 ㅇ 선형성 :[# αx[n]+βy[n] \; \longleftrightarrow \; αX(Ω)+βY(Ω) #]4. DTFT 수렴성 ㅇ x[n]이 절대 가합적 (absolutely summable)ㅇ 또는, x[n]이 유한 에너지를 갖는 에너지 신호일 경우
5. DTFT 변환 쌍
6. 타 변환 과의 관계 ㅇ 샘플링을 통한 CTFT, DTFT 관계
ㅇ DTFT 변환과 z 변환 관계
- DTFT는 z 변환의 특수한 경우로써, z 변환에서
으로 둔 것과 같음 . 즉, DTFT는 z 평면에서 단위 원주
에 대해서 만 z 변환한 것과 같음 7. 임펄스 응답 과의 관계 ㅇ 시간영역의 이산 임펄스응답 h[n]을 주파수영역의 DTFT 변환한 것이 주파수응답이 됨
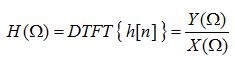
▷이산 푸리에 표현
1. DTFS (이산시간 푸리에급수) 2. DTFT (이산시간 푸리에변환) 3. 디지털 주파수 4.
▷이산푸리에변환 (DFT)
▷푸리에변환 표현 종류
1. CTFS(연속시간 푸리에급수) 2. CTFT(연속시간 푸리에변환) 3. DTFS(이산시간 푸리에급수) 4. DTFT(이산시간 푸리에변환) 5. DFT(이산푸리에변환) 6. FFT(고속푸리에변환) 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]