Observables, Operator 가 관측량, 관측 가능량, 연산자 | (2024-09-18) |
▷
Top
▷
기초과학
▷
물리
▷
양자 물리학
▷
파동함수, 파동방정식
1. [양자역학] 가 관측량(Observables) ㅇ 고전역학에서의 측정 가능한 동역학적인 변수(물리량)들 - 위치, 선운동량, 각운동량, 에너지 등 2. [양자역학] 연산자 ㅇ 연산자 이란? - 함수나 벡터에 작용하여 다른 함수나 벡터로 변환시키는 규칙(작용소) ㅇ 양자역학의 연산자 - 물리적 관측량(위치,운동량,에너지 등)을 수학적으로 표현하고, - 이를 계의 상태에 적용하여, 해당 물리량의 값을 추출하는 도구 . 선형 연산자로 취급됨 . 파동 함수,상태 벡터에 작용하여, 새로운 함수,상태를 생성하거나 결과를 예측하는 등 - 연산자 표현법을 위한 기본 가정 . 모든 측정가능한(관측가능한) 고전적인(동역학적) 물리량에 대응하는 연산자가 반드시 존재함 ㅇ 슈뢰딩거 방정식에 대한 연산자 표기 (고유값 방정식 형태)[# Hψ(x) = Eψ(x) #]- 전체 에너지 연산자/해밀토니안 연산자 : H . 계의 총 에너지를 나타내며, 일반적으로 운동 에너지와 위치 에너지의 합으로 구성[# H = -\frac{\hbar^2}{2m}\nabla^2 + V = \small{운동에너지} + \small{위치에너지} #]- 슈뢰딩거 방정식을 만족시키는 특정 에너지 E : 고유값 - 고유값 E에 대응하는 특정 함수 Ψ(x) : 고유함수 ㅇ 선운동량 연산자 : p[# \mathbf{p}ψ(x) = pψ(x) #]- 선운동량 연산자를 입자의 파동함수에 적용하면 운동량이 구해짐 ☞ 고유벡터 참조[# \mathbf{p} = -i\hbar\frac{d}{dx}\hat{\mathbf{x}}#]ㅇ 여러 관측가능 물리량에 대응하는 연산자들의 요약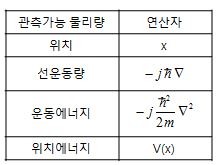
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]