Conditional Probability, Conditional PDF 조건 확률, 조건부 확률, 조건 확률밀도함수 | (2023-10-16) |
조건부 분포, 조건부 확률의 의의 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 변수
▷
이변량 랜덤변수
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 베이즈 통계학
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 베이즈 통계학
1. 조건부 확률 (Conditional Probability) ㅇ 어떤 좁혀진 조건 하에서 발생 확률 ㅇ (조건부 확률의 의의/의미) - 만일, 표본공간에 새로운 정보가 추가되면, . 그에 따라 갱신된 (좁혀진) 표본공간에서 구하게 되는 확률 - 이렇게, 매회(관측) 마다 달라진 조건 (좁혀진 부분을 전체로 간주함)에 따라, . 매번 좁혀진 범위에서, . (더 나은 특성을 갖는) 새로이 계산된 확률값을 취하는 방식 * [참고] ☞ 베이즈 통계 (베이즈 갱신), 우도 (가설에 대한 지지도) 참조 2. 조건부 확률의 정의 및 표기 ㅇ P(B|A) = P(A∩B) / P(A) (여기서, P(A) > 0) - P(B|A) : A 조건 하에 B가 일어날 조건부 확률 (Conditional Probability) . P(B)는, 표본공간 S에서 사건 B가 발생한 확률인 반면에, . P(B|A)는, 사건 A를 표본공간으로 취급하여 그 안에서 사건 B가 발생한 확률임 - P(A,B) = P(AB) = P(A∩B) : 함께/동시에 일어날 결합 확률 (Joint Probability) - P(A) : 특정 사건 A에 만 주목한 주변 확률 (Marginal Probability) ㅇ 例) S = {1,2,3,4,5,6}, A = {2,4,6}, B = {4,5,6} 이면, - 전체 확률 : P(S) = 6/6 = 1 - 결합 확률 : P(A∩B) = 2/6 = 1/3 - 주변 확률 : P(A) = 3/6 = 1/2, P(B) = 3/6 = 1/2 - 조건부 확률 . P(B|A) = P(A∩B) / P(A) = {4,6} / {2,4,6} = 2/3 . P(A|B) = P(A∩B) / P(B) = {4,6} / {4,5,6} = 2/3 3. 독립사건(Independent) 및 종속사건(Dependent)에서의 조건부확률 ㅇ 사건 A,B가 독립사건이면, - P(A|B) = P(A) 또는 P(B|A) = P(B) ㅇ 사건 A,B가 종속사건이면, - P(A|B) = P(A,B) / P(B) 또는 P(B|A) = P(B,A) / P(A) 4. 조건 확률분포 ㅇ 조건 확률누적분포함수 (Conditional CDF)- 성질
ㅇ 조건 확률밀도함수 (Conditional PDF)
- 성질
ㅇ 다변량 조건 확률밀도함수 (Multivariate Conditional PDF) - Xk+1,Xk+2,...,Xp가 주어졌을 때의 조건부 확률밀도함수
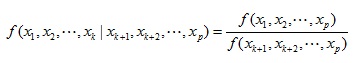
▷이변량 랜덤변수
1. 이변량 랜덤변수 2. 결합 확률/분포/모멘트 3. 결합 누적분포함수 4. 결합 확률질량함수 5. 결합 확률밀도함수 6. 주변 확률 7. 조건 확률 8. 독립,종속,배반,결합 사건
▷베이즈 통계학
1. 베이즈 통계 2. 베이즈 정리 3. 사전확률/사후확률 4. 조건부 확률 5. 우도 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]