Matrix Multiplication, Matrix Product 행렬 곱셈 | (2022-04-04) |
행렬 곱, 행렬의 곱, 행렬들의 곱, 행렬 벡터 곱 | |
▷
Top
▷
기초과학
▷
수학
▷
대수학
▷
선형 대수학
▷
행렬
▷
행렬 연산
1. 행렬 곱셈 이란? ㅇ 의미 - 두 행렬에서 좌측 행렬의 행(row)에 우측 행렬의 열(column)을 곱하는 것- 즉, 각각의 두 벡터(행 벡터,열 벡터)를 곱하는 내적과 같음 ㅇ 표기 : AB - 두 행렬 사이에 연산자 없이, 그냥 AB 라고 나타냄 ㅇ 성분 : cij - {# c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} = \sum_{k=1}^n a_{ik}b_{kj} #} . 즉, A의 i번째 행 벡터와 B의 j번째 열 벡터의 내적 임 ㅇ 크기 : (m x n) - (m x r) 행렬 A와 (r x n) 행렬 B의 곱 => (m x n) 행렬 AB
[# \begin{matrix} A & B & = & C \\ (m \times r) & (r \times n) & & (m \times n) \end{matrix} #]. 즉, A의 열의 개수 r = B의 행의 개수 r 이어야 함 ㅇ 존재성 - 반드시, 행렬 A의 열의 갯수가 행렬 B의 행의 갯수와 같아야 함 . 만일, 곱해지는 두 행렬 크기가 다르면 행렬 곱셈은 존재하지 않음 ※ [참고] ☞ 행렬곱셈 알고리즘, 행렬 곱셈 실제 구현 참조 2. 행렬 곱셈의 성질 ㅇ 비 가환적임 (not communicative) : AB ≠ BA - 즉, 교환법칙이 성립하지 않음 (곱해지는 순서가 중요 함) ㅇ 결합법칙,분배법칙 성립함 - 곱셈 결합법칙 : A(BC) = (AB)C - 스칼라 결합 곱셈 : k(AB) = (kA)B = A(kB) - 좌 분배법칙 : A(B+C) = AB + AC - 우 분배법칙 : (A+B)C = AC + BC ㅇ 곱셈 항등원 : In A = A = A In (A의 크기는 n x n) ㅇ 행렬 지수 곱셈 : Ak = A A ... A (행렬 A가 k번 곱해짐) 3. 행렬 곱셈의 의의 ㅇ 행렬 곱셈은, - 단순히, 수들을 곱하여 얻어진다는 것 그 이상으로, - `일차변환(선형변환)`에 사용할 수 있게 하는 수학적 도구 임 ㅇ 예를들면,[#(AB)\mathbf{x}#]는, - 행렬곱셈 (AB)가 벡터 x에 작용하는 어떤 형태의 합성함수로 볼 수 있음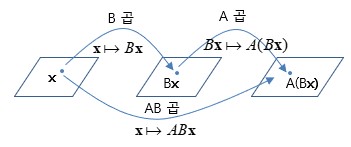 [# A(B\mathbf{x}) = (AB)\mathbf{x} \\ \qquad B\mathbf{x} = \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] \mathbf{x} = \mathbf{b}_1\mathbf{x}_1+\mathbf{b}_2\mathbf{x}_2+\cdots+\mathbf{b}_n\mathbf{x}_n \\ \qquad A(B\mathbf{x}) = A \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] \mathbf{x} \\ \qquad AB = A \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] = \left[\begin{array}{c|c|c|c} A\mathbf{b}_1 & A\mathbf{b}_2 & \cdots & A\mathbf{b}_n \end{array}\right] \\ \qquad AB\mathbf{x} = \left[\begin{array}{c|c|c|c} A\mathbf{b}_1 & A\mathbf{b}_2 & \cdots & A\mathbf{b}_n \end{array}\right] \mathbf{x} #]4. 행렬 곱셈의 열 또는 행 표현법 ※ ☞ 행렬 곱셈의 열 표현, 행렬 곱셈의 행 표현 참조 - 통상, 행렬 곱셈은 응용 관점에서 `열 관점 표현`을 많이 씀
[# A(B\mathbf{x}) = (AB)\mathbf{x} \\ \qquad B\mathbf{x} = \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] \mathbf{x} = \mathbf{b}_1\mathbf{x}_1+\mathbf{b}_2\mathbf{x}_2+\cdots+\mathbf{b}_n\mathbf{x}_n \\ \qquad A(B\mathbf{x}) = A \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] \mathbf{x} \\ \qquad AB = A \left[\begin{array}{c|c|c|c} \mathbf{b}_1 & \mathbf{b}_2 & \cdots & \mathbf{b}_n \end{array}\right] = \left[\begin{array}{c|c|c|c} A\mathbf{b}_1 & A\mathbf{b}_2 & \cdots & A\mathbf{b}_n \end{array}\right] \\ \qquad AB\mathbf{x} = \left[\begin{array}{c|c|c|c} A\mathbf{b}_1 & A\mathbf{b}_2 & \cdots & A\mathbf{b}_n \end{array}\right] \mathbf{x} #]4. 행렬 곱셈의 열 또는 행 표현법 ※ ☞ 행렬 곱셈의 열 표현, 행렬 곱셈의 행 표현 참조 - 통상, 행렬 곱셈은 응용 관점에서 `열 관점 표현`을 많이 씀
▷행렬 연산
1. 행렬 연산 2. 블록 행렬 3. 행렬 곱셈 4. 행렬 곱셈의 열/행 표현 5. 행렬 곱셈 알고리즘