Function Mapping Transformation 함수 사상 변환 | (2020-05-01) |
변환/사상/함수, 변환 매핑 함수 연산 투영 코딩 비교, 대응 관계 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분적분
▷
함수
▷
변환 매핑 함수 연산 투영 코딩
1. 변환, 매핑, 함수, 연산, 투영, 코딩 비교 ※ 이들 용어 모두 사실상 거의 같은 의미를 갖으며, - 수학/과학/기술 각 분야에서 관례적으로 용어를 각각 선호하며, - 특정 의미를 강조하며 사용되고 있음 ㅇ (분야별 공통적인 의미) - 공간 간에 대응관계 - 이 공간에서 저 공간으로 갈 때, 내용상 동등하나 표현은 달라짐 - 1 이상의 대상들을 결합시켜 또다른 결과를 내놓는 것 ㅇ (분야별 선호되는 의미) - 선형대수학에서는, `함수`,`사상` 보다는 `변환`이라는 용어를 주로 사용 . 입력과 출력 모두가 벡터 또는 행렬인 경우에 주로 변환이라고 함 - 기하학에서는, `함수` 보다는 `사상`,`변환`,`투영` 이라는 용어를 주로 사용 - 변환은, 주로 이를통해 해석이 용이해지거나 취급이 단순해지게 하는 것을 말함 - 함수는, 多:1 또는 1:1과 같이 1개 결과 만을 내놓는 것일 때를 말함 - 매핑은, 수학적으로는 함수와 비슷하나, 함수보다는 더 일반적인 개념으로 봄 - 연산은, 타 공간이 아닌, 자신이 속해있는 공간 그 자체로 보내지는 것을 말함 - 투영은, n 차원에서 (n-1) 차원 미만으로 차원을 단순화시키는 것을 말함 - 코딩은, 1개 부호어(부호화 단위)로써 대응되는 심볼에 할당하는 것을 말함 2. 수학적으로, 다음과 같이 다양한 표현이 가능 ㅇ f는 집합 X에서 집합 Y로의 함수ㅇ 집합 X의 각 원소 x가 집합 Y에 있는 하나의 특별한 원소 f(x)로의 사상
- 여기서, 값 f(x)는 함수 f가 만드는 x의 상(image)이라고함
. 정의역 : 집합 X . 공역 : 집합 Y . f의 치역 : 정의역에 있는 모든 점들의 상(image)으로만 이루어진 공역의 부분집합 ㅇ 벡터 x로부터 벡터 y로 보내는 변환
ㅇ 두 집합 간 대응관계 종류
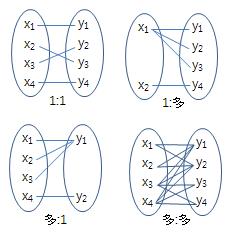
▷변환 매핑 함수 연산 투영 코딩
1. 변환 매핑 함수 연산 투영 코딩 비교 2. 변환 (Transformation) 3. 사상 (Mapping) 4. 연산 (Operation) 5. 투영 (Projection)