Orthogonal, Orthogonality 직교성, 직교 | (2023-07-28) |
직교성 판단 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
신호 표현/성질
▷
직교성
▷ Top ▷ 기초과학 ▷ 수학 ▷ 기초수학 ▷ 비교 (같음/닮음/다름)
▷ Top ▷ 기초과학 ▷ 수학 ▷ 대수학 ▷ 선형 대수학 ▷ 직교성
▷ Top ▷ 기초과학 ▷ 수학 ▷ 대수학 ▷ 선형 대수학 ▷ 벡터 ▷ 벡터의 크기,각도,거리,직교,투영
▷ Top ▷ 기초과학 ▷ 수학 ▷ 기초수학 ▷ 비교 (같음/닮음/다름)
▷ Top ▷ 기초과학 ▷ 수학 ▷ 대수학 ▷ 선형 대수학 ▷ 직교성
▷ Top ▷ 기초과학 ▷ 수학 ▷ 대수학 ▷ 선형 대수학 ▷ 벡터 ▷ 벡터의 크기,각도,거리,직교,투영
1. 직교성 (Orthogonality)
ㅇ 의미
- 수학적으로, 각 요소들이 서로 독립적임을 나타내는 용어
- 일반적으로, 신호/현상 상호 간에 전혀 관련성이 없음을 의미
※ `직교`의 어원
- 그리스어 `orthos` : 곧은(straight),옳은/정확한(right,true),직각을 이루는 등을 의미
- 직교(直交) : `직각(直角)으로 만나다(交)`의 뜻
※ `직각`,`직교` 용어 차이
- 둘 다 같은 의미를 갖으나,
* 직각(perpendicular)은, 기하학적인 용어이고,
* 직교(orthogonal)는, 기하학 및 대수학 등 모두를 포괄하는 광의의 용어
※ `직교성`,`상관성` 용어 차이
- `직교성` <-(반대)-> `상관성`
. 통상, 수치 `0`에 가까우면 직교적이고, 수치 `1`에 가까우면 상관적 이라고 말함
※ `직교성`,`상관성` 등 비교의 개념에 대한 폭넓은 이해는, ☞ 비교(같음/닮음/다름) 참조
2. 벡터, 함수 등에서 직교성 판단
ㅇ 벡터 직교성의 판단
- 두 벡터의 내적(Inner Product/Dot Product)이 `0`
. {# < \mathbf{x},\mathbf{y} > \;=\; \mathbf{x} \cdot \mathbf{y} \;=\; \mathbf{x}^T \mathbf{y} \;=\; 0 #}
* `내적`이라는 수치값에 의해,
. `벡터`가 비로소 기하학적인 의미(크기,각도,거리 등 스칼라량)를 부여 받음
* 만일, 두 벡터가 직교하면, 다음의 피타고라스 정리가 성립함
. {# || \mathbf{u} + \mathbf{v} ||^2 = ||\mathbf{u}||^2 + ||\mathbf{v}||^2 #}
ㅇ 함수 또는 신호 직교성의 판단
- 두 함수를 곱하여 적분한 결과가 `0`
. 실수 함수
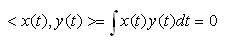 . 복소수 함수
. 복소수 함수
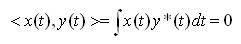 - 유한구간 (a,b)에서의 직교성
- 유한구간 (a,b)에서의 직교성
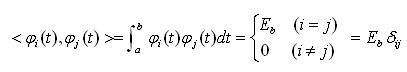 * 대표적인 직교성 검토 例) (정현파 신호,복소지수 신호)
* 대표적인 직교성 검토 例) (정현파 신호,복소지수 신호)
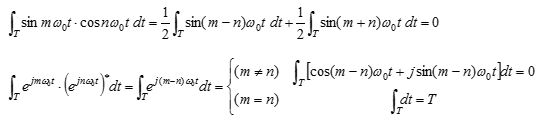 ㅇ 행렬 직교성의 판단
- 두 행렬 간의 행렬 곱셈한 결과가 `0 벡터 (영벡터)`
. A ·B = 0
3. 직교 집합, 직교 공간 이란?
※ ☞ 직교 집합 (Orthogonal Set), 직교 공간 (Orthogonal Space) 참조
- 집합 : 범위가 확정된, 구체적인 대상이 정해진 어떤 요소들의 모음
- 공간 : 집합의 요소들이 어떤 대수적 구조를 갖는 틀 내에서 그려내는 공간
- 생성 : 집합이 어떤 규칙에 따라 공간을 생성함
- 직교 : 구성 요소들 간에 서로 독립적/관계없음
4. 분야별 직교성 의미
ㅇ [신호 해석 분야] `직교(直交)`
- 어떤 신호들이 무리를 이루고 있을 때 이 무리에 속한 임의의 두 신호를 선택하더라도,
- 이 두 신호가 서로 직교함(독립적임)
. 어느 하나의 신호라도 신호 무리들 중 다른 신호들의 결합된 형태로 표현 못함
.. 직교 신호 例) cos (2πfct) 및 cos (2πfct + 90˚) = - sin (2πfct)
ㅇ [푸리에 급수] `신호의 푸리에급수 표현`
- 직교기저 함수인 정현파 또는 지수신호들의 무한 집합을 이용하여,
- 주기신호를 무한급수 형태로 표현
ㅇ [통신 변조 분야] `동위상 (In-phase)` 및 `직교위상 (Quadrature)`
- 위상이 상호 직각(90˚)으로 직교한다는 의미로써,
- 동위상(In-phase) 및 직교위상(Quadrature) 으로 구분 가능
* [참고] ☞ 직교위상변조(QM), 복소포락선, 직교위상천이변조(QPSK) 등 참조
ㅇ [코드 분야] `직교 코드 (Orthogonal Code)`
- 서로 다른 코드 사이에 상호상관이 0 인 코드를 말함 ☞ 왈쉬코드(Walsh Code) 참조
ㅇ 행렬 직교성의 판단
- 두 행렬 간의 행렬 곱셈한 결과가 `0 벡터 (영벡터)`
. A ·B = 0
3. 직교 집합, 직교 공간 이란?
※ ☞ 직교 집합 (Orthogonal Set), 직교 공간 (Orthogonal Space) 참조
- 집합 : 범위가 확정된, 구체적인 대상이 정해진 어떤 요소들의 모음
- 공간 : 집합의 요소들이 어떤 대수적 구조를 갖는 틀 내에서 그려내는 공간
- 생성 : 집합이 어떤 규칙에 따라 공간을 생성함
- 직교 : 구성 요소들 간에 서로 독립적/관계없음
4. 분야별 직교성 의미
ㅇ [신호 해석 분야] `직교(直交)`
- 어떤 신호들이 무리를 이루고 있을 때 이 무리에 속한 임의의 두 신호를 선택하더라도,
- 이 두 신호가 서로 직교함(독립적임)
. 어느 하나의 신호라도 신호 무리들 중 다른 신호들의 결합된 형태로 표현 못함
.. 직교 신호 例) cos (2πfct) 및 cos (2πfct + 90˚) = - sin (2πfct)
ㅇ [푸리에 급수] `신호의 푸리에급수 표현`
- 직교기저 함수인 정현파 또는 지수신호들의 무한 집합을 이용하여,
- 주기신호를 무한급수 형태로 표현
ㅇ [통신 변조 분야] `동위상 (In-phase)` 및 `직교위상 (Quadrature)`
- 위상이 상호 직각(90˚)으로 직교한다는 의미로써,
- 동위상(In-phase) 및 직교위상(Quadrature) 으로 구분 가능
* [참고] ☞ 직교위상변조(QM), 복소포락선, 직교위상천이변조(QPSK) 등 참조
ㅇ [코드 분야] `직교 코드 (Orthogonal Code)`
- 서로 다른 코드 사이에 상호상관이 0 인 코드를 말함 ☞ 왈쉬코드(Walsh Code) 참조
▷직교성
1. 직교성 2. 직교 집합 3. 정규 직교
▷비교 (같음/닮음/다름)
1. 비교 이란? 2. 동치 3. 합동 4. 닮음 5. 합동,닮음 간의 비교 6. 상관 7. 차이 8. 직교(직각)
▷직교성
1. 직교성 2. 그람 슈미트 직교화 과정 3. 일차, 이차 형식
▷벡터의 크기,각도,거리,직교,투영
1. 내적 2. 크기(노름) 3. 거리 4. 직교 5. 외적 6. 투영 7. 슈바르츠 부등식 8. 피타고라스 정리 용어해설 종합 (단일 페이지 형태)
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]