MGF Moment Generating Function 적률 생성 함수 | (2019-11-08) |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
통계량
1. 적률 생성 함수 (MGF) ㅇ 주어진 확률분포에서 적분이나 합을 구함이 없이 적률을 생성시키는 함수 - 다양한 형태의 적률들을 하나의 함수에 모두 표현 가능하게 함 ㅇ 정의식 - 적률을 생성할 수 있는 특별한 함수(esX)의 기대값 . MX(s) = E[esX] (E[] : 기대값, X : 랜덤변수, s : 실수값) - 이산,연속 랜덤변수의 기대값* (유의점) 기대값 표현식이 라플라스 변환 형태와 유사함 2. 적률생성함수 성질/특징 ㅇ 확률변수들의 선형결합의 분포를 나타내는데 유용 ㅇ 확률밀도함수(PDF) 또는 확률질량함수(PMF)의 (주파수)변환 - 즉, 적률생성함수(MGF)는 확률밀도함수(PDF)/확률질량함수(PMF)와 변환 쌍 관계를 이룸 ㅇ r차 적률
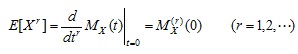
▷통계량
1. 통계량 2. 모멘트(원점적률,중심적률) 3. 적률생성함수 4. 비율