Priori Probability, Posteriori Probability 사전 확률, 선험적 확률, 사후 확률, 후험적 확률 | (2025-03-10) |
수정 확률, 역 확률 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
통계학
▷
베이즈 통계학
1. 사전 확률, 선험적 확률 (Priori Probability) ㅇ 실제 확률 실험 시행 전에(관측전에), 사건 발생에 대해 이미 알고 있는 확률(믿음) - 관측전 현재 정보를 기초로하여 정하는 초기 확률(믿음) . 이는 경험,직관 등에 의해 이미 알고있는 확률(믿음)임 ㅇ 例) - 공정한 6면 주사위에서, 특정 숫자가 나올 사전 확률은 모두 같음. P(1) = P(2) = ... = 1/6 - 공정한 동전에서, 앞면 또는 뒷면이 나올 사전 확률은 같음. P(Head) = P(Tail) = 1/2 - 특정 질병에 걸릴 확률이 0.1% 라면, 어떤 사람이 검사 전 사전 확률은, P(특정 질병) = 0.001 ※ 여기서의 확률(믿음)은, 시행전 갖을 수 있는, 주관적 확률을 의미함 - 이는 시행 후, 상대 빈도로써 확정되는, 객관적 확률과는 다름 . (확률의 종류 셋(3) : 이론적 확률, 객관적 확률, 주관적 확률) 2. 사후 확률, 후험적 확률, 수정 확률, 역 확률 (Posteriori Probability) ㅇ 사건 발생 후에(관측후에), 그것이 어떤 원인일 것이라고 생각되는(기대되는) 확률 - 즉, 결과로부터 원인이 무엇일까라는 역방향 확률 (Inverse Probability) ㅇ 사후 확률은 직접 구하기 어려워, 사전 확률 및 기타 정보로부터 이를 계산해 냄 ☞ 아래 3.항 - 주어진 사전 확률로부터, 이를 관측하던중에, - 어떤 조건이 부과되었을 때, 그렇게 기대되는 확률 값을 계산할 수 있음 ㅇ 때론, 수정 확률 / 갱신 확률 (Updated Probability) 이라고도 함 - 즉, 추가된 정보(관측 결과)로부터, 사전 확률를 새롭게 수정/정제하여, . 이를 통해 사후 수정 확률을 얻어냄 - 이렇게 구하는 과정을 `베이즈 갱신 (Bayesian Updating)` 이라고도 함 - 여기서, 베이즈 갱신 이란? . 앞의 정보를 이용하여, 다음 사후 수정 확률 계산을 위한 사전 확률로 사용함을 말함 3. 사후 확률의 표현식 => 베이즈 정리 ㅇ `사후 확률 P(A|B)`을, `사전 확률 P(A),P(B)과 조건부 확률 P(B|A)`로부터 구할 수 있음[# P(A_i|B_j) = \frac{P(B_j|A_i)P(A_i)}{P(B_j)} #]- 여기서, {# P(B_j) = \sum^M_{i=1}P(B_j|A_i)P(A_i) #} (전체 확률의 정리) 4. 위의 사후 확률의 표현식에서, 항목별 설명 ㅇ A : 원인, 가정, 가설 ㅇ B : 관측, 결과 ㅇ i = 1,2,...,M : 가설(원인) 종류 (분류 범주/분류 영역/클래스/카테고리 등) ㅇ j = 1,2,... : 관측(샘플)들 ㅇ P(Ai|Bj) : 사후 확률 (조건부확률 : 원인의 확률) - 관측 B를 보고 원인이 A라고 생각되는(기대되는) 확률 ㅇ P(Ai) : 사전 확률 - 원인/소스별로 이미 알고있는 확률 (또는, 초기 믿음) ㅇ P(Bj|Ai) : 우도 (조건부 확률 : 결과의 확률) - 각각의 원인 Ai로부터 결과 Bj가 나타날 것이라는 가설에 대해 지지하는 정도 - 나타난 결과 마다 다른 값을 갖는, 여러 가능한 가설들을 평가할 수 있는 조건부확률 ㅇ P(Bj) : 해당 결과가 나오도록 모든 원인들 마다 기여하는 확률들의 합 - 이는, 사후 확률의 값을 정확히 구하는 계산에는 필요한 값이나, - 주로, 사후 확률의 크기 비교에 의해 추론/결정/판정을 하므로, 이에 영향을 미치지 않아서, - 통상, 정규화된 상수로 취급하거나 무시함 ㅇ 한편, 많은 문제에서, 원인이 각 결과에 기여하는 정도가 같고, 정적인 경우가 많으므로, - 사전 확률을 계산에 포함(고려) 않음 ㅇ 한편, `사전 확률`,`우도`는 사전에 훈련 집합을 통해서 구해질 수 있음 5. 한편, 사후 확률을 다음과 같이 표현도 가능 ㅇ 우도 (Likelihood,조건부 확률), 사전 확률 (Priori), 증거 (Evidence)에 의해서도 표현 가능[# P(ω_i|\mathbf{x}) = \frac{P(\mathbf{x}|ω_i)P(ω_i)}{P(\mathbf{x})} \qquad \text{posteriori} = \frac{\text{likelihood} \times \text{priori}}{\text{evidence}} #]- ωi : 분류 범주/분류 영역/클래스/카테고리 등 (i = 1,2,...,M) - x : 관측 벡터 6. 사후 확률의 계산 例) ※ 만일, 결정 규칙(결정 전략)을 세우려면, - 각 관측 결과 마다 분류범주 M 번의 확률 계산을 해야 함 - 例) 관측 결과가 2진수(참/거짓)일 경우에, 2 x M 번의 확률 계산을 하고 살펴보아야 함 . 이때, 각 결과에서 계산된 사후 확률 값 중 가장 큰 것(가설)을 취하는 것이 합리적임 .. (사후 확률의 계산은, 베이즈 정리에 따른 위 3,4,5항 참고) . 이를두고 최대 사후확률 규칙 이라고 함 ㅇ 아래의 2진 채널에서, 사후확률을 구해보면,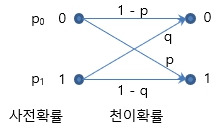 [# P(X=0|Y=0) = \frac{P(Y=0|X=0)P(X=0)}{P(Y=0)} \\ \qquad\qquad\qquad\quad = \frac{P(Y=0|X=0)P(X=0)}{P(Y=0|X=0)P(X=0)+P(Y=0|X=1)P(X=1)} \\ \qquad\qquad\qquad\quad = \frac{(1-p)p_0}{(1-p)p_0 + qp_1} #][# P(X=1|Y=1), P(X=0|Y=1), P(X=1|Y=0) #]도 마찬가지로 구하면 됨
[# P(X=0|Y=0) = \frac{P(Y=0|X=0)P(X=0)}{P(Y=0)} \\ \qquad\qquad\qquad\quad = \frac{P(Y=0|X=0)P(X=0)}{P(Y=0|X=0)P(X=0)+P(Y=0|X=1)P(X=1)} \\ \qquad\qquad\qquad\quad = \frac{(1-p)p_0}{(1-p)p_0 + qp_1} #][# P(X=1|Y=1), P(X=0|Y=1), P(X=1|Y=0) #]도 마찬가지로 구하면 됨
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]