Spherical Coordinate System 구 좌표계, 구면 좌표계 | (2019-05-11) |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
좌표계
1. 구 좌표계/구면 좌표계 (Spherical Coordinate System) (r,θ,Φ) ㅇ 2차원 극좌표계를 => 3차원으로 확장시켜 일반화시킨 좌표계 - r (원점 반경), θ (선택된 축에서 각도), Φ (그 축 둘레의 방위각)2. 직각좌표계와의 관계 ㅇ x = r sinθcosΦ, y = r sinθsinΦ, z = r cosθ ㅇ r = √(x2 + y2 + z2), tanΦ = y / x, tanθ = √(x2 + y2) / z ※ ☞ 직교 좌표계 변환 (Orthogonal Coordinate System Transformation) 참조 3. 구 좌표계 주요 특징 ㅇ 미소 입체각 : dΩ = sinθdθdΦ [sr] ㅇ 미소 면적소 : dA = r2 sinθdθdΦ [㎡] ㅇ 미소 체적소 : dV = r2sinθdrdθdΦ [㎥] ㅇ 구 전체 표면적 : A = 4πr2 [㎡] ※ ☞ 원통 좌표계 참조 4. 구좌표계에서 시간 미분(속도,가속도) ㅇ 1차 시간 미분(속도) :
ㅇ 2차 시간 미분(가속도) :
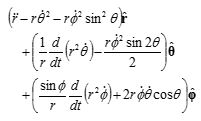
▷좌표계
1. 좌표계 2. 직교 좌표계 3. 직각 좌표계 4. 극 좌표계 5. 원통 좌표계 6. 구 좌표계 7. 기저벡터 좌표계 8. 경로 좌표계