Taylor Series, Maclaurin series 테일러 급수, 매클로린 급수 | (2023-11-21) |
Taylor Expansion, 테일러 전개, Taylor Polynomial, 테일러 다항식, Taylor Approximation, 테일러 근사 | |
▷
Top
▷
기초과학
▷
수학
▷
기초수학
▷
수열,급수
▷
멱급수
1. 테일러 급수(Taylor Series), 테일러 급수 전개(Taylor Series Expansion) ㅇ 함수를 멱급수 (다항식) 형태로 표현 (근사)하는 방법 - 수치적으로 정확하게 다루기 어려운 함수들에 대해, - 도함수가 포함된 다항식 형태로 근사화하는 방법 (다항식 근사) ※ Brook Taylor (1685~1731) : 영국 수학자 (Newton의 후계자임을 자청) 2. 테일러 급수의 용도 ㅇ 함수를 근사화시킬 수 있음 - (도함수 포함 멱급수 형태로써) ㅇ 함수 값을 근사적으로 구할 수 있음 - 어떤 점에서의 함수값을, 그의 도함수값들을 사용하여, 근사시킴 ㅇ 근사의 정확성(오차 크기) 정도를 어림할 수 있음 3. 테일러 급수의 특징 ㅇ 급수의 각 항 계수들이 그 함수의 도함수와 관련되어짐 - 만일, f(x)가 중심 a에서 해석적(무한번 미분가능 등)이면 다음과 같이 표현 가능[# f(x) = \sum^{\infty}_{k=0} \frac{f^{(k)}(a)}{k!} (x-a)^k #]. 위 식은, 중심 a에 관한 어떤 개구간에서도 성립됨 . 한편, 점 a는, 중심점 또는 동작점 또는 기준점 이라고도 불리움 ㅇ [참고] - 매끄러운(해석적) 함수에 대해서는, 항상, 멱급수(또는 다항식) 형태로 전개 가능 4. 테일러 급수 및 매클로린 급수의 전개 ※ (어떤 한 점의 함수값에 대한, 멱급수 근사 또는 전개) ㅇ 테일러 급수 (Taylor Series) 근사 또는 전개 - 어떤 한 점의 함수값에 대해, 중심점 a에서의 함수값과 그 미분값들로 표현 .[# f(x) = f(a) + (x-a)f'(a) + \frac{(x-a)^2}{2!}f''(a) + \cdots = \sum^{\infty}_{n=0}\frac{(x-a)^n}{n!}f^{n}(a) #].[# f(x+dx) = f(x) + (dx)f'(x) + \frac{(dx)^2}{2!}f''(dx) + \cdots #].[# f(a+h) = f(a) + (h)f'(a) + \frac{(h)^2}{2!}f''(a) + \cdots #]ㅇ 매클로린 급수 (Maclaurin series) 근사 또는 전개 - (중심 a = 0 일 때의 테일러급수 전개와 같음) .[# f(x) = \sum^{\infty}_{n=0}\frac{x^n}{n!}f^{(n)}(a) #]5. 테일러 다항식 (Taylor Polynomial) : Tn(x) ㅇ 테일러 급수를 유한개 항의 다항식 만으로 나타낸 것 - n번째까지 만의 급수 합 (n차 다항식)ㅇ 근사값 계산에 이용됨 - n → ∞ 이 됨에 따라, Tn(x) → f(x) 6. 테일러 급수의 근사값 ㅇ x = xi+1 근방의 f(x)에 대한 근사를, - x = xi를 중심으로 0차,1차,2차,..,n차 등으로, 근사하는 例
7. 테일러 근사의 오차 : Rn(x) ㅇ f(x) = Tn(x) + Rn(x) - Tn(x) : 테일러 다항식
- Rn(x) : 테일러 급수의 나머지항(remainder) 또는 절단오차 . 오차의 크기와 관련됨
8. 주요 멱급수 (Maclaurin 급수) 표현 ☞ 급수 공식 참조
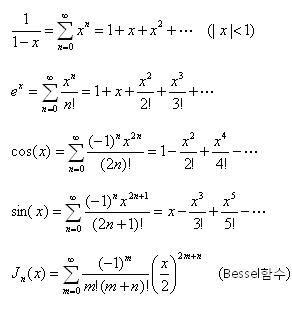
▷멱급수
1. 멱 급수 2. 멱급수 공식 3. 삼각 급수 4. 테일러 급수 5. 푸리에 급수