Covariance, Correlation Coefficient 공 분산, 상관 계수 | (2024-02-03) |
통계적 유사도, 통계 상관 계수, 피어슨 상관 계수 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
신호 표현/성질
▷
상관성
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 통계적 분석 ▷ 상관분석
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 통계적 분석 ▷ 상관분석
1. 데이터(변량) 간에 통계적 유사성의 정량화 ㅇ 단일 변량의 산포 정도 ☞ 분산 참조 ㅇ 2 변량 간의 상관관계 정도 : 공분산, 상관계수(정규화된 공분산) - 여기서의 상관계수는, Karl Pearson의 적률 상관계수(피어슨 상관계수)를 말함 . 다만, 두 변량이 모두, .. 연속적, 선형 관계, 양적 데이터 일 때 만 그 관계를 제대로 보여줌 ㅇ 2 이상의 다 변량 간의 상관관계 정도 - 2 이상의 다 변량 간의 상관 계수 : 다중 상관계수, 편 상관계수, 정준 상관계수 등 - 2 이상의 질적 변수들 간의 상관 계수 : 파이 계수, 분할 계수, 순위 상관계수(스피어만,켄달) 등 - 2 이상의 다 변량 간에 공분산의 행렬 표현 ☞ 확률 벡터, 공분산 행렬 참조 ㅇ 변량 간의 산포/상관의 일반화 ☞ 상관성(Correlation) 참조 2. 공 분산 (Covariance) ㅇ 두 변량이 상관적으로 변화되는 척도 - 두 변량(확률변수) 간에 상관성/의존성/유사성의 `방향` 및 `정도`에 대한 척도 . 두 변량 (Variate) 간에 직선적 상관관계 (Correlation)의 측도 (Measure) ㅇ 공 분산의 표현식 - 편차곱 {#(x_i-\bar{x})(y_i-\bar{y})#}의 평균 . 두 변량이 각각의 평균으로부터 변화하는 방향 및 크기를 보여줌[# \frac{(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+\cdots+(x_n-\bar{x})(y_n-\bar{y})}{n} #]ㅇ 공 분산의 표기 : 보통, Cov(X,Y), σXY, sXY로 표시함 - 이산형[# Cov[X,Y]=σ_{XY} = E[(X-μ_X)(Y-μ_Y)] = \sum_x \sum_y (x-μ_X)(y-μ_Y) p(x,y) #]- 연속형[# Cov[X,Y]=σ_{XY} = E[(X-μ_X)(Y-μ_Y)] = \int^{\infty}_{-\infty} \int^{\infty}_{-\infty} (x-μ_X)(y-μ_Y) f(x,y) dxdy #]ㅇ 공 분산의 성질 - 교환법칙 성립 .[# Cov[X,Y] = Cov[Y,X] #]- 동일 변량에 대한 공분산은 분산이 됨 .[# Cov[X,X] = Var[X] #]- 간편 계산을 위한 형식 . {# Cov[X,Y]=σ_{XY} = E[(X-μ_X)(Y-μ_Y)] = E[XY] - μ_Xμ_Y #} - 두 변량이 상호독립이면, 공분산은 0 이 됨 . {# Cov[X,Y]=0 #} - 기타 성질 .[# Cov[aX+b,cY+d] = ac \; Cov[X,Y] #]ㅇ 다 변량 확률변수의 공 분산 ☞ 공분산 행렬, 상관계수 행렬 참조 - 2 변량 이상의 변량이 있는 경우에, - 모든 변량 쌍들 간의 공분산을 행렬로 표현한 것 3. 상관 계수 (Correlation Coefficient) = 정규화된 공분산 ㅇ 공분산이 각 변량의 단위에 의존하게되어 변동 크기량이 모호하므로, - 공분산에다가 각 변량의 표준편차들의 곱으로 나누어주어 `정규화`시킴[# ρ = Corr(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)}\sqrt{Var(Y)}} = \frac{σ_{XY}}{σ_{X}σ_{Y}} #]- 여기서, Var() : 분산, σX : 표준편차, Cov(X,Y) : 공분산 ㅇ 특징 - 단위가 무차원(dimensionless)임 - 값 범위 : -1 ≤ ρ ≤ 1 ※ (명칭) 이같은 통계적 상관계수를, 제안자 이름을 따서, - `피어슨의 적률 상관계수` 또는 `피어슨 상관 계수` 라고도 함 4. 공 분산 또는 상관 계수 값에 따른 의미 ㅇ 양의 상관 : `강한 양의 상관관계` = (공분산 > 0) (positively correlated) - 두 변량이 같은 방향으로 움직임 (X가 커지면 Y도 덩달아 커짐 : 오른쪽으로 증가) . 만일, 두 변량이 크기도 같고, 같은 방향이면, ρ = 1 이 됨 (직선에 가까움) ㅇ 영의 상관 : `상관관계 없음` = (공분산 = 0) (uncorrelated) - 두 변량이 상호 독립 (상관관계가 전혀 없음 : 넓게퍼짐) . 만일, 두 변량이 상관 없으면, ρ = 0 이 됨 .. 즉, 통계적 독립인 경우 임[# E[(X-μ_X)(Y-μ_Y)] = E[X-μ_X]E[Y-μ_Y] = 0 #]ㅇ 음의 상관 : `강한 음의 상관관계` = (공분산 < 0) (negatively correlated) - 두 변량이 반대방향으로 움직이는 것 (X가 커지면 Y는 작아짐 : 왼쪽으로 감소) . 만일, 두 변량이 크기는 같으나, 다른 방향이면, ρ = -1 이 됨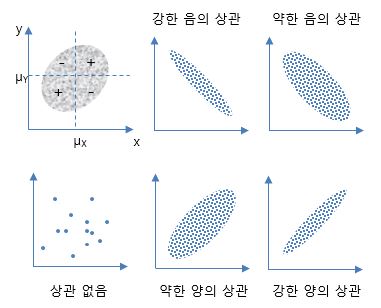
▷상관성
1. 상관성 2. 상관기(수신기) 3. 공분산,상관계수
▷상관분석
1. 상관성 2. 상관분석 3. 공분산,상관계수 4. 공분산 행렬