Definite Integral 정 적분 | (2023-08-07) |
Integrable, 적분 가능Mensuration by parts, 구분 구적법, Riemann Summation, 리만 합 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분적분
▷
적분
▷
정적분
1. 구분 구적법 (Mensuration by Parts) 이란?
ㅇ 구적법 (Mensuration)
- 실용적인 필요에 의해, 도형의 넓이,부피를 구하기 위해, 고대로부터 고안된 방법들을 일컬음
ㅇ 구분 구적법 (Mensuration by Parts)
- 도형의 넓이나 부피를,
. 세분화된 분할 도형 (삼각형,직사각형,정사각형 등) 각각의 넓이의 합을 구하고,
. 그 합의 극한으로, 전체 도형의 넓이,부피를 구하는 방법을 지칭
- 기본적으로, 넓이를 폭이 없는 선으로, 부피는 두께가 없는 면들의 모임으로 간주함
2. 정 적분 (Definite Integral)
ㅇ 적분 구간이 정해지어 그 결과가 상수값이 되는 적분
ㅇ 폐구간 [a,b]에서 적분 가능한 함수 f(x)의 정 적분 정의
[# I = \lim_{n \to \infty} \sum^n_{k=1} f(x^*_k) Δx = \int^b_a f(x) dx #]
- ∫ : 적분 기호 (`적분`,`Integral`이라고 읽음)
- f(x) : 피 적분 함수 (Integrand)
- a : 적분 하한 (lower limit of integration)
- b : 적분 상한 (upper limit of integration)
- x : 적분 변수
ㅇ 일변수 함수에서, 정해진 적분 구간 내에 정 적분을 취하면, 넓이를 구할 수 있음
3. 정 적분 가능 (Integrable)
ㅇ 구간 [a,b]에서 정의되는 함수 f에 대해,
- 정적분 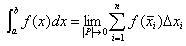 이 존재하면,
. 여기서, |P|는 분할구간,
이 존재하면,
. 여기서, |P|는 분할구간, 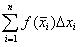 은 리만합(Riemann Summation)
- 이때, 함수 f는 구간 [a,b]에서 적분가능한 함수라고 함
* 리만 합 : 잘게 분할한 구간 마다의 함수 값들의 합으로 적분 값(정적분)을 근사시키는 방법
. 리만(Riemann,1826~1866) : 독일 수학자
.. 적분의 정의를 일반화시켰고, 복소함수의 기하학적인 이론의 토대를 닦음
ㅇ 직관적으로, 적분 가능 함수는 넓이를 잘 정의할 수 있음을 의미
4. 정 적분의 성질
[# \int^b_a f(x) dx = - \int^a_b f(x) dx \qquad (a < b) \\
\int^a_a f(x) dx = 0 \\
\int^b_a k dx = k(b-a) \\
\int^b_a kf(x) dx = k \int^b_a f(x)dx \\
\int^b_a (αf(x)+βg(x))dx = α\int^b_a f(x)dx + β\int^b_a g(x)dx \\
\int^b_a f(x)dx = \int^c_a f(x)dx + \int^b_c f(x)dx #]
5. 다변수 함수의 적분
※ ☞ 중 적분 참조
- 선 적분, 면 적분, 체적 적분
은 리만합(Riemann Summation)
- 이때, 함수 f는 구간 [a,b]에서 적분가능한 함수라고 함
* 리만 합 : 잘게 분할한 구간 마다의 함수 값들의 합으로 적분 값(정적분)을 근사시키는 방법
. 리만(Riemann,1826~1866) : 독일 수학자
.. 적분의 정의를 일반화시켰고, 복소함수의 기하학적인 이론의 토대를 닦음
ㅇ 직관적으로, 적분 가능 함수는 넓이를 잘 정의할 수 있음을 의미
4. 정 적분의 성질
[# \int^b_a f(x) dx = - \int^a_b f(x) dx \qquad (a < b) \\
\int^a_a f(x) dx = 0 \\
\int^b_a k dx = k(b-a) \\
\int^b_a kf(x) dx = k \int^b_a f(x)dx \\
\int^b_a (αf(x)+βg(x))dx = α\int^b_a f(x)dx + β\int^b_a g(x)dx \\
\int^b_a f(x)dx = \int^c_a f(x)dx + \int^b_c f(x)dx #]
5. 다변수 함수의 적분
※ ☞ 중 적분 참조
- 선 적분, 면 적분, 체적 적분
▷정적분
1. 정적분 2. 수치 적분 3. 넓이 4. 부피