Transformation 변환 , 변환 (Transformation) | (2022-08-11) |
변환 영역, 영역 변환, 좌표 변환 | |
▷
Top
▷
전기전자공학
▷
신호 및 시스템
▷
변환 해석
▷ Top ▷ 기초과학 ▷ 수학 ▷ 해석학(미적분 등) ▷ 미분적분 ▷ 함수 ▷ 변환 매핑 함수 연산 투영 코딩
▷ Top ▷ 기초과학 ▷ 수학 ▷ 해석학(미적분 등) ▷ 미분적분 ▷ 함수 ▷ 변환 매핑 함수 연산 투영 코딩
1. 변환 (Transformation)
ㅇ 표현하는 영역을 바꾸어 달리 표현한다는 광의의 용어
- 이 공간에서 저 공간으로 달리 표현할 수 있으나, 내용상으로는 동등함
. 즉, 여러 좌표 공간을 정의하고, 이들 간에 표현 방법을 달리하는 것
ㅇ 이를통해, 해석이 용이해지거나 취급이 단순해지는 등 여러가지 장점이 있음
2. 변환의 수학적 표기
ㅇ 공간 간의 변환 표현
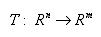 ㅇ 벡터 간의 변환 표현
ㅇ 벡터 간의 변환 표현
 - 입력과 출력 모두가 벡터인 경우에 주로 `변환`이라고 함
. 이때의 벡터 변환 표기로는 통상적으로 대문자 T, F, L 등을 사용함
ㅇ 점(변수) 간의 함수적 변환 표현
- 입력과 출력 모두가 벡터인 경우에 주로 `변환`이라고 함
. 이때의 벡터 변환 표기로는 통상적으로 대문자 T, F, L 등을 사용함
ㅇ 점(변수) 간의 함수적 변환 표현
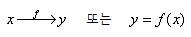 3. `함수(Function)`, `사상(Mapping)`, `변환(Transformation)`
※ ☞ 함수 사상 변환 참조
- 세 용어 모두 사실상 거의 같은 의미를 갖음
. 수학 각 분야에서 관례적으로 세 용어를 각각 선호하며 사용하고 있음
. 선형대수학에서는 `함수`,`사상` 보다는 `변환`이라는 용어를 더 선호
4. 변환의 종류 例)
ㅇ 표현식 변환
- 표현 식을 바꿈 (깔끔하고 직관적 이해가 가능한 수식 유도 등)
ㅇ 좌표 변환 : 서로 다르게 정의된 좌표계 간의 좌표 변환
- 공간 내 동일한 점의 서로다른 좌표계 간에 좌표를 바꾸는 것 例) 직교 좌표계 변환 등
ㅇ 합동 변환(등거리 변환, Isometry) : 위치를 바꾸어도 정확히 포개지는 변환
- 유클리드 공간에서 점 사이의 길이를 변하지 않게하는 변환
ㅇ 선형 변환 (linear transformation) : 선형적 성질을 유지하는 변환
- 벡터 공간의 수학적 구조를 보존하는 변환
. 벡터공간 간에 2가지 연산(벡터합,스칼라곱) 성질을 보존하며 변환
ㅇ 영역 변환 : 해석의 용이성을 추구하는 변환 (주로,주파수 영역 변환)
- 때론, 적분 변환(Integral Transform) 이라고도 함
- 주로, 시간 영역에서 신호의 표현/해석을 주파수 영역으로 바꾸어서 쉽게 표현/해석
* 신호처리 분야에서 시간영역과 변환영역(주로,주파수영역) 간의 관계에 대한 이해가 매우 중요
. 특히, 시스템 입출력 간의 응답 관계를 쉽게 표현시켜줌
* [참고] ☞ 주파수영역변환(푸리에변환,라플라스변환,z변환),복소주파수,시스템응답 등 참조
ㅇ 기하학적 그래픽 변환 (Geometric Graphic Transformation) : 영상 내 화소의 재배치 변환
- 영상 내 화소의 공간적 위치를 재배치하는 것
. 영상 내 물체 간의 기하학적 관계를 변환시킴으로써, 화소의 재배치
. 영상 객체의 크기,위치,방향 등을 변환시킴
.. 이동(translation),회전(rotation),스케일링(scaling) 등
- 점 변환,도형 변환 등
. 점을 한 점에서 다른 점으로 옮김 (점을 대응시키는 사상)
. 도형을 다른 형태의 도형으로 바꿈 (도형의 단순화,취급 용이 등)
ㅇ 영상 변환 (Image Transform) : 영상 정보를 다른 형태의 정보로 변환
- 영상 정보를 공간 영역이 아닌 다른 영역(주파수영역 등)으로 변환시켜서,
. 영상의 개선, 압축, 해석 등을 수행
* [참고] ☞ 영상 변환, 변환 부호화(DCT 변환,푸리에 변환,웨이블릿 변환 등) 참조
ㅇ 코드 변환 (Code Transformation) : 응용에 맞도록 코드 변환
- 주어진 응용에 적합토록 코드(부호)의 속성 및 효율적인 코드 변환
ㅇ 로그 변환 (Log Transformation)
- 곱셈을 덧셈으로 변환시킴으로써,
- 매우 큰 수 또는 극미한 수를 계산 취급하는데, 많은 편리함을 주는 수 표현 방식
3. `함수(Function)`, `사상(Mapping)`, `변환(Transformation)`
※ ☞ 함수 사상 변환 참조
- 세 용어 모두 사실상 거의 같은 의미를 갖음
. 수학 각 분야에서 관례적으로 세 용어를 각각 선호하며 사용하고 있음
. 선형대수학에서는 `함수`,`사상` 보다는 `변환`이라는 용어를 더 선호
4. 변환의 종류 例)
ㅇ 표현식 변환
- 표현 식을 바꿈 (깔끔하고 직관적 이해가 가능한 수식 유도 등)
ㅇ 좌표 변환 : 서로 다르게 정의된 좌표계 간의 좌표 변환
- 공간 내 동일한 점의 서로다른 좌표계 간에 좌표를 바꾸는 것 例) 직교 좌표계 변환 등
ㅇ 합동 변환(등거리 변환, Isometry) : 위치를 바꾸어도 정확히 포개지는 변환
- 유클리드 공간에서 점 사이의 길이를 변하지 않게하는 변환
ㅇ 선형 변환 (linear transformation) : 선형적 성질을 유지하는 변환
- 벡터 공간의 수학적 구조를 보존하는 변환
. 벡터공간 간에 2가지 연산(벡터합,스칼라곱) 성질을 보존하며 변환
ㅇ 영역 변환 : 해석의 용이성을 추구하는 변환 (주로,주파수 영역 변환)
- 때론, 적분 변환(Integral Transform) 이라고도 함
- 주로, 시간 영역에서 신호의 표현/해석을 주파수 영역으로 바꾸어서 쉽게 표현/해석
* 신호처리 분야에서 시간영역과 변환영역(주로,주파수영역) 간의 관계에 대한 이해가 매우 중요
. 특히, 시스템 입출력 간의 응답 관계를 쉽게 표현시켜줌
* [참고] ☞ 주파수영역변환(푸리에변환,라플라스변환,z변환),복소주파수,시스템응답 등 참조
ㅇ 기하학적 그래픽 변환 (Geometric Graphic Transformation) : 영상 내 화소의 재배치 변환
- 영상 내 화소의 공간적 위치를 재배치하는 것
. 영상 내 물체 간의 기하학적 관계를 변환시킴으로써, 화소의 재배치
. 영상 객체의 크기,위치,방향 등을 변환시킴
.. 이동(translation),회전(rotation),스케일링(scaling) 등
- 점 변환,도형 변환 등
. 점을 한 점에서 다른 점으로 옮김 (점을 대응시키는 사상)
. 도형을 다른 형태의 도형으로 바꿈 (도형의 단순화,취급 용이 등)
ㅇ 영상 변환 (Image Transform) : 영상 정보를 다른 형태의 정보로 변환
- 영상 정보를 공간 영역이 아닌 다른 영역(주파수영역 등)으로 변환시켜서,
. 영상의 개선, 압축, 해석 등을 수행
* [참고] ☞ 영상 변환, 변환 부호화(DCT 변환,푸리에 변환,웨이블릿 변환 등) 참조
ㅇ 코드 변환 (Code Transformation) : 응용에 맞도록 코드 변환
- 주어진 응용에 적합토록 코드(부호)의 속성 및 효율적인 코드 변환
ㅇ 로그 변환 (Log Transformation)
- 곱셈을 덧셈으로 변환시킴으로써,
- 매우 큰 수 또는 극미한 수를 계산 취급하는데, 많은 편리함을 주는 수 표현 방식
▷변환 해석
1. 변환 이란? 2. 주파수 영역 3. 복소 주파수 영역
▷변환 매핑 함수 연산 투영 코딩
1. 변환 매핑 함수 연산 투영 코딩 비교 2. 변환 (Transformation) 3. 사상 (Mapping) 4. 연산 (Operation) 5. 투영 (Projection)