Vector Function Derivative 벡터 함수 미분, 벡터 함수 도함수, 벡터 미분 | (2018-03-18) |
스칼라장의 미분, 스칼라장의 도함수, 벡터장의 미분, 벡터장의 도함수 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
벡터해석학
1. 벡터 함수의 미분 (또는 도함수) ㅇ 벡터함수 내 각 성분함수를 미분함으로써 얻어지는 벡터함수ㅇ 이렇게 얻어진 `벡터함수의 미분(도함수)`는, - r(t)로 정의되는 곡선의 어떤 점에서의 `접선 벡터(Tangential Vector)`가 됨 - 이를 `속도 벡터(Velocity Vector)` 라고도 함 2. 벡터 미분의 물리적 의미 => 물체의 운동 표현 가능 ※ 공간,평면 영역에서 움직이는 물체의 운동(속도,가속도,회전 등) 표현 가능 - [직각좌표계 표현] ☞ 속도벡터,가속도벡터 참조 - [극좌표계 표현] ☞ 원운동 벡터 표현 참조 ㅇ 회전하는 벡터함수의 시간 미분 및 그 성질(의미)
- 벡터의 크기가 일정(dA/dt=0)하고 방향 만 변하면, . 원래 벡터의 수직인 벡터가 됨 즉,
3. 벡터 함수의 미분 공식 ㅇ 상수 벡터의 미분 :
ㅇ 벡터의 스칼라 곱셈의 미분 :
ㅇ 스칼라함수,벡터함수 곱의 미분 :
ㅇ 벡터함수 합의 미분 :
ㅇ 벡터함수 내적의 미분 :
ㅇ 벡터함수 외적의 미분 :
ㅇ 벡터함수의 연쇄법칙 :
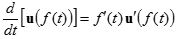
▷벡터해석학
1. 벡터 해석학 2. 벡터 함수 3. 벡터 함수 미분 4. 위치/속도/가속도 벡터 5. 원운동 벡터 표현 6. 주요 벡터공식