Bessel Function 베셀 함수, Bessel 함수 | (2021-06-07) |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분방정식
▷
특수함수
1. 베셀 함수(Bessel Function) 이란? ㅇ 원통형 대칭성을 갖는 문제를 다룰때 나타나는 전형적인 특수 함수 - 例) 행성 운동을 기술하는 케플러 방정식을 풀 때 나타나는 등 ㅇ 다음과 같은 베셀 미분방정식의 해로써 나타나는 함수[# x^2 y'' + x y' + (x^2 - \mu^2) y = 0 #]ㅇ 다니엘 베르누이가 처음으로 정의하고, 베셀이 일반화시킴 - 베셀 (Bessel, Friedrich Wilhelm, 1784~1846) 독일 천문학자 2. 베셀 함수 종류 ㅇ 1종 베셀함수 Jμ(x) - 모든 실수 μ에 대해, x=0 에서 유한한 값을 갖는 Jμ(x)- 성질 . 모든 x에 대해 수렴 . x≪1에서 J0(x)가 큰 값을 갖음 . x가 증가함에 따라 Jμ(x)가 발진하지만 점차 진폭이 감소함 . Jμ(x)의 최대값은 μ가 증가함에 따라 감소함 ㅇ 2종 베셀함수 Yμ(x) - 모든 실수 μ에 대해, x=0 에서 특이점(값)을 갖는 Yμ(x)
- 성질 . x=0 에서 무한대로 발산 . 일명 베버함수(Weber Function),노이만함수(Neuman Function)라고도 불리움 3. 베셀 함수의 성질 (Jμ 또는 Yμ) ㅇ 기초사항
ㅇ 도함수
ㅇ 점화관계(recursion)
- J0(x),J1(x)로부터 모든 μ에 대해 구할 수 있음 4. 베셀 함수의 생성, 적분표시, 수열근사 ㅇ 베셀함수의 생성함수
ㅇ 베셀함수의 적분표시
ㅇ 베셀함수의 수렴근사
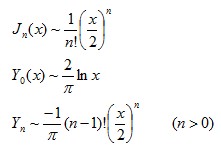
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]