Limit, Continuity 극한, 연속 | (2023-07-26) |
Limit Value, 극한값, Indeterminate Form, 부정형 | |
▷
Top
▷
기초과학
▷
수학
▷
해석학(미적분 등)
▷
미분적분
▷
극한, 연속, 발산
1. 극한에 대한 직관적 정의
ㅇ 극한 (Limit) 또는 극한값 (Limit Value) 이란?
- 일변수 함수의 극한
. x가 a에 한없이 가까워질 때, 함수값 f(x)가 어떤 극한(값) L이 됨
[# \lim_{x \to a} f(x) = L #]
- 이변수 함수의 극한
. (x,y)가 (a,b)에 한없이 가까워질 때, 함수값 f(x,y)가 어떤 극한(값) L이 됨
[# \lim_{(x,y) \to (a,b)} f(x,y) = L #]
2. 극한의 용도 및 응용
ㅇ 극한의 유용성
- 독립변수가 어떤 값에 접근할 때, 그에따른 함수의 변동성을 서술하는데 유용
ㅇ 극한 개념의 응용
- 곡선의 접선 등을 구하기 위해 필요함
- 움직이는 물체의 순간 속도(순간 변화율)을 알아내기 등
3. 극한의 존재성(Existence)
ㅇ 극한이 존재하면, ⇒ 미분가능 하다고 함
- 즉, 극한의 존재는 함수 f가 점 a에서 미분가능(f is differential at a) 함을 의미
. 이 경우, 함수가 갑자기 점프하거나,한없이 증가 또는 감소하는 등을 하지 않음
ㅇ 극한의 존재성 확인
- 좌극한과 우극한이 같아야 함
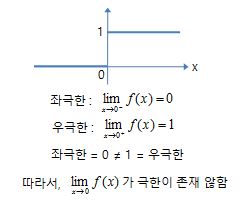 ※ 한편, limx→0 sin x / x = 1 과 같은 경우를 증명하려면,
- 극한에 대한 더욱 엄밀한 증명이 필요함
※ 한편, 다변수 함수의 극한의 존재성은, 좌극한,우극한 만 고려하는 일변수 함수와는 달리,
- 모든 방향에서 접근 가능하게 됨
4. 극한과 연속
ㅇ 연속 (Continuity)
- 극한과 함수값이 같으면, 함수는 그 점에서 연속임
[# \lim_{x \to a} f(x) = f(a) #]
※ 연속과 극한의 개념은 서로 밀접하게 맞닿아있음
5. 극한과 발산,수렴
ㅇ 발산(Divergence)
- 만일, 극한이 무한으로 커지면, 발산 한다고 함
ㅇ 수렴(Convergence)
- 만일, 극한이 어떤 값에 한없이 가까워지면, 수렴 한다고 함
6. 극한의 성질(법칙)
ㅇ 합의 법칙 :
※ 한편, limx→0 sin x / x = 1 과 같은 경우를 증명하려면,
- 극한에 대한 더욱 엄밀한 증명이 필요함
※ 한편, 다변수 함수의 극한의 존재성은, 좌극한,우극한 만 고려하는 일변수 함수와는 달리,
- 모든 방향에서 접근 가능하게 됨
4. 극한과 연속
ㅇ 연속 (Continuity)
- 극한과 함수값이 같으면, 함수는 그 점에서 연속임
[# \lim_{x \to a} f(x) = f(a) #]
※ 연속과 극한의 개념은 서로 밀접하게 맞닿아있음
5. 극한과 발산,수렴
ㅇ 발산(Divergence)
- 만일, 극한이 무한으로 커지면, 발산 한다고 함
ㅇ 수렴(Convergence)
- 만일, 극한이 어떤 값에 한없이 가까워지면, 수렴 한다고 함
6. 극한의 성질(법칙)
ㅇ 합의 법칙 : 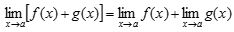 ㅇ 차의 법칙 :
ㅇ 차의 법칙 : 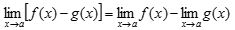 ㅇ 상수 곱셈의 법칙 :
ㅇ 상수 곱셈의 법칙 : 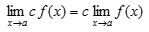 ㅇ 곱의 법칙 :
ㅇ 곱의 법칙 : 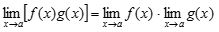 ㅇ 몫의 법칙 :
ㅇ 몫의 법칙 : 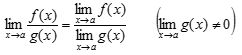 7. 부정형 (Indeterminate Form)
ㅇ 함수의 극한을 구할 때, 분모/분자 또는 곱해지는 또는 지수 항이 0 또는 ∞이 되어서,
함수의 극한을 쉽게 결정할 수 없는 형태들을 말함
- f(x)/g(x) => 0/0, ∞/∞
- f(x)·g(x) => 0·∞
- f(x) - g(x) => ∞ - ∞
- [f(x)]g(x) => 00, ∞0, 1∞
7. 부정형 (Indeterminate Form)
ㅇ 함수의 극한을 구할 때, 분모/분자 또는 곱해지는 또는 지수 항이 0 또는 ∞이 되어서,
함수의 극한을 쉽게 결정할 수 없는 형태들을 말함
- f(x)/g(x) => 0/0, ∞/∞
- f(x)·g(x) => 0·∞
- f(x) - g(x) => ∞ - ∞
- [f(x)]g(x) => 00, ∞0, 1∞
"본 웹사이트 내 모든 저작물은 원출처를 밝히는 한 자유롭게 사용(상업화포함) 가능합니다"
[정보통신기술용어해설]