Standard Normal Distribution, Standard Gaussian Distribution 표준 정규분포, 표준 가우시안 분포 | (2024-02-12) |
Z 분포, Z 변환, 표준 정규분포표 읽는 법 | |
▷
Top
▷
기초과학
▷
수학
▷
확률/통계
▷
확률 모형,분포
▷
정규분포
▷
표준 정규분포
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 통계적 추론 ▷ 표본 분포,표본 통계량 ▷ 표본 분포
▷ Top ▷ 기초과학 ▷ 수학 ▷ 확률/통계 ▷ 통계학 ▷ 통계적 추론 ▷ 표본 분포,표본 통계량 ▷ 표본 분포
1. 표준 정규분포 (Standard Normal Distribution) ㅇ 정규분포를 규격화시킨 것 - 다양한 종(Bell) 모양의 정규분포를, - `평균 μ이 0` 이고 `표준편차 σ가 1` 로써, 규격화시킨 것 2. 표준 정규분포로의 변환 필요성 ㅇ 정규분포(가우시안 분포)의 불편함 - 평균 및 표준편차 값에 따라 중심 위치 및 전체 모양이 달라짐 . 2 이상의 정규분포를 서로 비교할 때 또는 확률값 계산할 때에 매우 불편 ㅇ 따라서, 모든 정규분포를 다음과 같이 표준적인 정규분포로 변환하여 사용이 바람직 - 즉, 평균이 0 이고, 표준편차가 1로 변환된 정규화된 분포 => 표준 정규분포 . 어떤 관찰값이 평균으로부터 표준편차의 몇 배 만큼 떨어져 있는가의 척도ㅇ `표준 정규분포` 및 `정규분포` 공통점 - 평균을 중심으로 좌우대칭이고 종 모양을 하는 점이 똑같으며, - 또한, 전체 면적이 1 이고, 각 σ 만큼의 면적이 변환 전후에도 같음 3. 확률변수의 표준화 (Standardized Random Variable) ㅇ 정규분포의 확률변수 X를 변환시켜, 평균 μ= 0, 분산 σ2= 1 이 되도록, 표준화시킨 확률변수 - 이러한 표준화/정규화 변환을 `Z 변환`이라고도 함 ☞ 표준화 변량, z 값 참조 ㅇ 즉, 확률변수 X의 표준화(정규화)된 Z 변환은,
[# Z_i = \frac{X_i - μ}{σ} #]- Z : 표준화된 변량 (표준 정규 확률변수) - X : 확률변수(변량), μ : 기대값 또는 평균, σ : 표준편차 ㅇ 역으로, 일반 정규분포의 데이터 값은,[# X_i = Z_iσ + μ #]4. 표준 정규분포 상의 확률값(면적값) 구하기 : (표준 정규분포표 읽는 법) ㅇ (표준 정규분포표 읽는 법) - 면적 (확률값) 읽기 => 대부분의 통계책 부록에 있는 `표준 정규분포표 (Z table)`을 이용 - 표준 정규분포표 (Z-table) : 특정 Z 값(z값)에서의 면적 수치(확률값)를 표로써 보여줌 . 세로축 : z값을 소수 첫째 자리까지 나타냄 . 가로축 : z값을 소수 둘째 자리까지 나타냄 . 표 안의 값 .. 세로,가로축 z값에 해당하는 확률, 즉 P(0 < Z < z) 확률 값 (누적 확률 값) .. 때론, P(Z > z) 확률 값 (상위 확률 값) ㅇ 자주 쓰이는 누적 확률 값 - 0.05 % : P(Z ≤ 1.645) = 0.95 - 0.025 % : P(Z ≤ 1.96) = 0.975 - 0.01 % : P(Z ≤ 2.326) = 0.99 - 0.005 % : P(Z ≤ 2.526) = 0.995 ㅇ `(평균 0) ± n x (표준편차 1)` 범위 내 면적은, 그 만큼의 확률값을 설명함 - 평균 0에서 ±3 범위 내 전체의 99.74% 가 존재 : P(- 3 < X̅ < + 3) = 0.9974 - 평균 0에서 ±2 범위 내 전체의 95.44% 가 존재 : P(- 2 < X̅ < + 2) = 0.9544 . 일반 정규분포의 확률변수로 나타낼 때는, -1.96 ≤ (X - μ)/σ ≤ +1.96 - 평균 0에서 ±1 범위 내 전체의 68.26% 가 존재 : P(- 1 < X̅ < + 1) = 0.6826 5. 표준 정규분포의 확률적 특성 ㅇ 표기 : X ~ N(0,1) - 평균 0, 분산 1 로써 표준화된 정규분포 ㅇ 확률밀도함수 : (PDF)[# f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \quad (-\infty < x < \infty) #]ㅇ 누적분포함수 : (CDF)[# F_X(x) = \int^x_{-\infty} f_X(x) dx = \int^x_{-\infty} e^{-\frac{x^2}{2}} dx #]※ 위 확률함수의 확률값은, 해석적이 아닌 수치적으로 구해짐 - 다음과 같이 Q 함수를 정의하여, 수치적으로 계산해 놓은 표를 찾아서 이용함 (위 4.항 참조)6. 일반 정규분포의 확률적 특성 ㅇ 표기 : X ~ N(μ,σ²) - 평균 μ, 분산 σ²인 정규분포 ㅇ 일반 정규분포의 확률밀도함수 : (PDF)
ㅇ 일반 정규분포의 누적분포함수 : (CDF)
ㅇ 일반 정규분포의 확률값
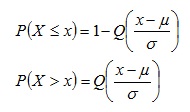
▷표준 정규분포
1. 표준 정규분포(Z 분포) 2. 표준화 변량, z 값 3. Q 함수 4. 오차함수
▷표본 분포
1. 표본 분포 2. 한 표본분포의 통계적 특성 3. 두 표본분포의 통계적 특성 4. Z 분포 5. t 분포 6. χ² 분포 7. F 분포